ДИСКРИМИНАНТ

ДИСКРИМИНАНТ - 1) Д. многочлена f(x) = , с а₀ ≠ 0, корни к-рого равны α₁, α₂, ... , α_n, - произведение

D(f) = a^2n-2₀ ∑_n≥u>j(α_i - α_j)².

Д. равен нулю тогда и только тогда, когда многочлен имеет кратные корни. Д. симметричен относительно корней многочлена и поэтому может быть выражен через его коэффициенты.

Д. квадратного трехчлена ах² + bx + с равен b² - 4ас; Д. многочлена x³ + px + q (корни к-рого вычисляются по Кардано формуле) равен -27q² - 4р³. Если f(x) - многочлен над полем характеристики 0, то

D(f) = (-1)^n(n-1)/2 a^-1 R(f, f'),

где R(f, f') - результант многочлена f(x) и его производной f'(x). Производной многочлена f(x) = a₀xⁿ + a₁x^n-1 ... + a_n с коэффициентами из любого поля наз. многочлен na₀x^n-1 + (n - 1)a₁x^n-2 + ... + a_n-1.

Лит.: [1] Куpош А. Г., Курс высшей алгебры, 11 изд., М., 1975.

И. В. Проскуряков.

2) Д. полуторалинейной формы f в базисе (v) = {v₁, ..., v_n} - элемент из кольца А, равный

  (*)

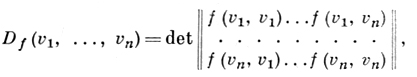где (v) - фиксированный базис конечномерного свободного А-модуля Е над коммутативным кольцом А с единицей, снабженным автоморфизмом σ. Если (w) = {w₁, ... , w_n} - другой базис в Е, а

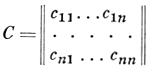
- матрица перехода от (v) к (w), то

D_f(w₁, ..., w_n) = (det С) (det С)^σ D_f(v₁, ..., v_n).

Если кольцо А не имеет делителей нуля, то для невырожденности f необходимо и достаточно, чтобы D_f(v₁, ..., v_n) ≠ 0.

Если v₁, ..., v_n - произвольный набор n элементов из Е, то элемент D_f(v₁, ..., v_n) кольца А, определяемый формулой (*), наз. дискриминантом f относительно системы v₁, ..., v_n. Пусть А без делителей нуля и f - невырожденная полуторалинейная форма. Тогда для того, чтобы система элементов v₁, ..., v_n из Е была свободной, необходимо и достаточно, чтобы D_f(v₁, ..., v_n) ≠ 0. При этом v₁, ..., v_n будет базисом в Е тогда и только тогда, когда D_f(v₁, ..., v_n) и D_f(u₁, ..., u_n) ассоциированны в А для некоторого базиса u₁, ..., u_n в А.

Лит.: [1] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [2] Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974.

В. Л. Попов.

3) Д. системы элементов поля - одна из важных конструкций в теории расширений полей. Пусть K - конечное расширение поля k степени n. Отображение K ×К в k:

(х, у) ↦ Тr(ху),

где х, у ∈ K, а Тr α — след элемента α ∈ К, является симметрической билинейной формой на поле K, рассматриваемом как линейное пространство над k. Д. этой билинейной формы (см. Дискриминант полуторалиней-ной формы) относительно системы элементов w₁, ..., w_m из K наз. дискриминантом системы w₁, ..., w_m и обозначается D(w₁, ..., w_m). В частности, если указанная система есть базис K над k, то ее Д. наз. дискриминантом базиса K над k. Д. двух базисов отличаются множителем, являющимся квадратом нек-рого ненулевого элемента поля k. Д. всякого базиса K над к не равен нулю тогда и только тогда, когда расширение К/k сепарабельно. Если f_x(t) — многочлен степени m, являющийся минимальным многочленом элемента х из сепарабельного расширения K/k, то D(1, х, х², х^m) совпадает с Д. многочлена f_x(t). Приведенные определения могут быть перенесены также на случай произвольной конечномерной ассоциативной алгебры над полем (см. ниже п. 4).

В случае сепарабельного расширения K/k Д. базиса w₁, ..., w_n может быть вычислен по формуле

D(w₁, ..., w_n) = (det(σ_i(w_j)))²,

где σ₁, ..., σ_n - все различные вложения К в фиксированное алгебраич. замыкание поля k, оставляющие неподвижным k.

Пусть k = ℚ - поле рациональных чисел, К - поле алгебраич. чисел и М - некоторый модуль ранга n в К. Тогда для любых двух базисов модуля М значения Д. совпадают и это общее значение Д. наз. дискриминантом модуля М. Если М совпадает с кольцом целых чисел поля K, то Д. модуля М наз. просто дискриминантом поля К и обозначается D_k. Число D_k является важной характеристикой поля К. Напр., если К допускает s вещественных и 2t комплексных вложений в поле комплексных чисел ℂ, то

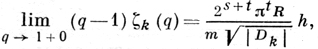
где ζ_k(q) - дзета-функция Дедекинда, h - число классов дивизоров, R - регулятор поля K и m - число корней из единицы в поле K. Имеется оценка

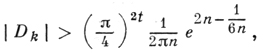
которая показывает, что lim_n→∞ |D_k| = ∞. Для квадратичного поля ℚ(√d), где d - свободное от квадратов целое рациональное число, d ≠ 1, имеют место формулы:

D_k = d, если d ≡ 1 (mod 4), D_k = 4d, если d ≡ 2 или 3 (mod 4).

Для кругового поля K = ℚ(ε), где ε - примитивный корень р^r-й степени из единицы

(знак минус берется при р^r = 4 или p ≡ 3(mod 4), а плюс - в остальных случаях).

Указанное определение Д. модуля в поле алгебраич. чисел может быть обобщено на тот случай, когда k -поле частных дедекиндова кольца А, а К - конечное сепарабельное расширение поля k степени n. Пусть В -целое замыкание кольца А в К и b - произвольный дробный идеал кольца В. Тогда дискриминантом идеала b наз. A-модуль D(b), порожденный всеми Д. вида D(w₁, ..., w_n), где {w₁, ... , w_n} пробегает всевозможные базисы поля К над k, лежащие в b. D(b) оказывается дробным идеалом кольца А, причем имеет место равенство D(b) = N(b)²D(В), где N(b) - норма идеала b. Д. D(В) совпадает с нормой дифференты кольца В над А.

Лит.: [1] Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Ленг С., Алгебраические числа, пер. с англ., М., 1966; [3] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [4] Джекобсон Н., Теория колец, пер. с англ., М., 1947.

В. Л. Попов.

4) Д. алгебры - Д. симметричной билинейной формы (х, у) = Т(ху), где х, у- элементы конечномерной ассоциативной алгебры А над полем F, а Т(а) -главный след элемента а ∈ А, определяемый следующим образом. Пусть е₁, ..., е_n - к.-л. базис алгебры А, Ф = F(ζ₁, ... , ζ_n) - чисто трансцендентное расширение поля F с помощью алгебраически независимых элементов ξ₁, ..., ξ_n, A_Ф = A_F ⊗ Ф - соответствующее скалярное расширение алгебры А, тогда элемент x = ξ₁e₁ + ... + ξ_ne_n ∈ A_Ф наз. общим элементом алгебры A, а минимальный многочлен (над Ф) элемента х - минимальным многочленом алгебры А. Пусть

g(t; ξ) = t^r - m₁(ξ)t^r-1 + ... + (-1)³m_r(ξ)

- минимальный многочлен алгебры A; коэффициенты m_i(ξ) оказываются на самом деле многочленами из F[ξ₁, ..., ξ_n]. Если а = α₁е₁ + ... + α_ne_n (α_i ∈ F) - произвольный элемент из А, то m₁(α₁, ..., α_m) = Т(а) наз. главным следом элемента a, m_r(α₁, ..., α_n) = N(a) - главной нормой, а многочлен g(t; α₁, ..., α_n) - главным многочленом. Коэффициенты главного многочлена для данного элемента а ∈ А не зависят от выбора базиса, поэтому упомянутая выше билинейная форма (х, у) на А определена инвариантно, в то время как ее Д. определен с точностью до мультипликативного множителя, являющегося квадратом ненулевого элемента из F. Алгебра А сепарабельна (см. Сепарабельная алгебра) тогда и только тогда, когда ее Д. отличен от нуля.

Лит.: [1] Джекобсон Н., Теория колец, пер. с англ., М., 1947.

Е. Н. Кузьмин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.