ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ

ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ - область математики, занимающаяся исследованием и решением экстремальных задач на конечных множествах. Пусть М = {а₁, а₂, ..., а_n} и f - числовая функция, определенная на элементах множества М. Требуется найти элемент а_j ∈ М, на к-ром достигается абсолютный минимум (или абсолютный максимум) f на М. Сокращенно такие задачи записываются:

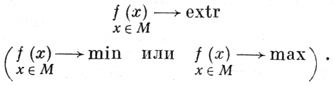
Из указанного класса задач Д. п. исследует только нетривиальные задачи, выделяемые следующими дополнительными условиями.

1. Число n = |M| должно быть достаточно большим настолько, чтобы задача не решалась непосредственным просмотром значений f(a_i) вручную или на ЭВМ. Так, в задаче коммивояжера, к-рая является типичной задачей Д. п., число вариантов Q при обходе m пунктов равно

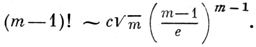
В задачах минимизации булевых функций (см. Булевых функций минимизация, Булевых функций метрическая теория) |М| > 2²ⁿ.

2. Задача не должна быть регулярной. Задача наз. регулярной, если: а) для каждого а_i ∈ М определена непустая окрестность S(a_i, М), и |S(a_i, M)| ≪ |M|; б) локальный экстремум f, т. е. точка а_i такая, что f(a_i) = extr f(x), x ∈ S(a_i, М), определяется при помощи простого алгоритма, в) локальный экстремум совпадает хотя бы с одним глобальным.

Таким образом, Д. п. рассматривает задачи, имеющие, вообще говоря, несколько локальных экстремумов. В типичных случаях число локальных экстремумов весьма велико. Напр., в задачах целочисленного линейного программирования с булевыми переменными, в к-рых функционал и ограничения зависят от переменных х₁, ..., х_k, число элементов в M не больше 2^k, а число локальных экстремумов может быть равным const ⋅ 2^k/√k (см. [2]). Трудность решения задач Д. п. и определяется наличием большого числа локальных экстремумов. Универсальных эффективных методов решения задач Д. п. не создано (1978). Как показывают исследования по минимизации булевых функций - хорошо исследованной модельной задаче Д. п. (см. также Алгоритм локальный), создание таких методов, по-видимому, невозможно. Методы, в достаточной степени универсальные, такие, как метод ветвей и границ (см. [1]) и его различные модификации, являются методами направленного перебора. Они эффективно применяются для решения специализированных задач Д. п. Однако для каждого из таких методов существуют обширные классы задач, для к-рых методы направленного перебора мало отличаются по сложности от методов полного перебора. Другой источник математич. трудностей в задачах Д. п. состоит в том, что множество М, на к-ром ищется экстремум f, часто задается в неявной форме. Так, в задачах целочисленного линейного программирования множество М определяется как совокупность целочисленных решении системы линейных неравенств. При таком и более сложных способах задания М нетривиальной становится не только задача полного перечисления М, но и указания хотя бы одного элемента из М. В силу изложенного, основные результаты Д. п. получены при решении и исследовании более узких классов задач. К таким классам относятся транспортная задача, задача о коммивояжере и нескольких коммивояжерах, линейное целочисленное программирование, задача о расписаниях (см. Расписаний теория), экстремальные задачи на графах (см. Графов теория), задачи минимального представления булевых функций и функций k-значной логики и т. д.

Другое направление в теории дискретных экстремальных задач состоит в развитии приближенных методов, обычно применяемых при решении практич. задач большой размерности. Принципиально эти методы не отличаются от соответствующих методов поиска экстремумов непрерывных функций и функционалов. В Д. п. используются аналоги алгоритмов локальной оптимизации, алгоритмов спуска, случайного поиска и т. п. (см. обзор приближенных методов решения задач Д. п. в [3]).

Интересным как с теоретич. точки зрения, так и в решении прикладных задач является статистический подход к задачам Д. п. Пусть совокупность задач {Z} можно представить в виде {Z} = ∪^∞_n=1 {Z}_n, где |{Z}_i| > |{Z}_j| при i > j и |{Z}_n| → ∞ при n → ∞. Говорят, что подмножество

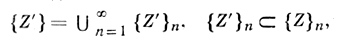
составляет почти все задачи Z, если

lim_n→∞ |{Z'}_n|/|{Z}| = 1.

Для различных классов задач Д. п. имеет место следующий факт: существует (а часто и эффективно описывается) совокупность {Z'} почти всех задач {Z}, для к-рых нахождение экстремума или хорошего приближения к экстремуму возможно в классе простых алгоритмов. Это было замечено впервые при решении задач синтеза оптимальных управляющих систем, напр. в минимизации булевых функций в классе дизъюнктивных нормальных форм, см. Булевых функций нормальные формы, а также [4]. Напр., задача выделения экстремальных конъюнкций, входящих хотя бы в одну минимальную дизъюнктивную нормальную форму булевой функции f(x₁, ..., x_n), неразрешима в классе локальных алгоритмов при k ⋅ l < const ⋅ 2ⁿ, где k - индекс локального алгоритма, l - величина памяти. В то же время задача выделения элементарных конъюнкций, входящих хотя бы в одну «почти минимальную» дизъюнктивную нормальную форму для почти всех булевых функций, разрешима в классе локальных алгоритмов при k = 2, l = 1 (см. [5]). Столь же значительное сокращение трудоемкости при переходе к почти всем задачам получается для экстремальных задач на графах, в задаче о построении оптимальных покрытий и т. д.

Лит.: [1] Корбут А. А., Финкельштейн Ю. Ю., Дискретное программирование, М., 1969; [2] Коробков В. К., «Проблемы кибернетики», 1965, в. 14, с. 297-99; [3] Финкельштейн Ю. Ю., Приближенные методы и прикладные задачи дискретного программирования, М., 1976; [4] Дискретная математика и математические вопросы кибернетики, т. 1, М., 1974; [5] Журавлев Ю. И., «Дискретный анализ», 1964, № 3, с. 41-77.

Ю. И. Журавлев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.