ДИСКРЕТНАЯ СЕРИЯ

ДИСКРЕТНАЯ СЕРИЯ представлений - семейство непрерывных неприводимых унитарных представлений локально компактной группы G, эквивалентных представлениям регулярного представления этой группы. Если группа G унимодулярна, то непрерывное неприводимое унитарное представление π группы G тогда и только тогда принадлежит Д. с, когда матричные элементы представления π лежат в L²(G). В этом случае существует такое положительное число d_π, называемое формальной размерностью представления π, что соотношения

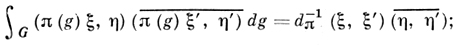  (1)

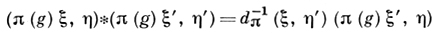  (2)

выполняются для всех векторов ξ, η, ξ', η' из пространства H_π представления π. Если π₁, π₂ - два неэквивалентных представления группы G в пространствах Н₁Н₂, соответственно, принадлежащие Д. с, то для любых ξ₁, η₁ ∈ H₁, ξ₂, η₂ ∈ H₂ выполняются соотношения

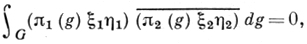  (3)

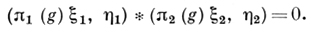  (4)

Соотношения (1)-(4) являются обобщениями соотношений ортогональности для матричных элементов представлений компактных топологич. групп (см. Представления компактных групп); группа G компактна тогда и только тогда, когда все непрерывные неприводимые унитарные представления группы G принадлежат Д. с, и если G компактна и мера Хаара dg удовлетворяет условию ∫_Gdg = 1, то число d_π совпадает с размерностью представления π. Односвязные нильпотентные вещественные группы Ли и комплексные полупростые группы Ли не имеют Д. с.

Класс эквивалентности представления π, входящего в Д. с., является замкнутой точкой в дуальном пространстве Ĝ группы G, и мера Планшереля этой точки совпадает с формальной размерностью d_π;если при этом нек-рый ненулевой матричный элемент представления π суммируем, то представление π является открытой точкой в носителе регулярного представления группы G, но открытые точки в Ĝ могут не соответствовать представлениям Д. с. Свойства представлений Д. с. частично распространяются на случай неунимодулярных локально компактных групп.

Лит.: [1] Диксмье Ж., С*-алгебры и их представления, пер. с фанц., М., 1974; [2] Harish-Chandra, «Acta Math.», 1965, v. 113, p. 241 - 318; 1966, v. 116, p. 1-111; [3] Schmid W., «Ann. Math.», 1976, v. 103, p. 375-94; [4] Kleppner A., Lipsman R., «Ann. sci. Ecole norm. sup.», 1972, t. 5, p. 459-516; 1973, t. 6, p. 103-32.

А. И. Штерн.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.