ДИСКРЕТНАЯ ПОДГРУППА

ДИСКРЕТНАЯ ПОДГРУППА - подгруппа Г топологич. группы G (в частности, подгруппа группы Ли), являющаяся дискретным подмножеством топологич. пространства G. В локально компактных топологич. группах (в частности, в группах Ли) выделяют решетки - Д. п., для к-рых факторпространство Г\G имеет конечный объем в смысле меры, индуцированной левоинвариантной Хаара мерой на группе G. К числу решеток относятся равномерные Д. п., для к-рых факторпространство Г\G компактно.

Если К - компактная подгруппа локально компактной топологич. группы G, то подгруппа T ⊂ G дискретна тогда и только тогда, когда она является дискретной группой преобразований пространства X = G/K (в смысле действия, индуцированного естественным действием группы G на X). При этом Г является решеткой (соответственно равномерной Д. п.) тогда и только тогда, когда факторпространство Г\X имеет конечный объем в смысле меры, индуцированной G-инвариаитной мерой на X (соответственно компактно). Это дает возможность использовать при изучении Д. п. групп Ли геометрии, методы.

Одна из основных задач теории Д. п. групп Ли -классификация таких подгрупп с точностью до соизмеримости. Подгруппы Г₁, Г₂ группы G наз. соизмеримыми, если Г₁ ∩ Г₂ имеет конечный индекс как в Г₁, так и в Г₂. Если одна из соизмеримых подгрупп локально компактной топологич. группы является Д. п. (соответственно решеткой, равномерной Д. п.), то и другая обладает этим свойством.

До середины 20 в. рассматривались в основном отдельные классы Д. п. групп Ли, обязанные своим происхождением арифметике, теории функций и физике. Исторически первая нетривиальная Д. п.- подгруппа SL₂(ℤ) группы SL₂(ℝ), названная впоследствии модулярной группой Клейна - фактически рассматривалась Ж. Лагранжем (J. Lagrange) и К. Гауссом (С. Gauss) в их исследованиях по арифметике квадратичных форм от двух переменных. Ее естественным обобщением является подгруппа SL_n(ℤ) группы SL_n(ℝ). Исследование этой группы как дискретной группы преобразований пространства положительно определенных квадратичных форм от n переменных составило предмет теории приведения, разработанной А. Н. Коркиным, Е. И. Золотаревым, Ш. Эрмитом (Ch. Hermite), Г. Минковским (Н. Minkowski) и др. во 2-й пол. 19 - начале 20 вв. Ряд арифметически определяемых Д. п. классич. групп Ли: группы единиц квадратичных форм с рациональными коэффициентами, группы единиц простых алгебр над ℚ, группу целочисленных симплетич. матриц - исследовал в 40-х гг. 20 в. К. Зигель (С. Siegel). Он, в частности, доказал, что все эти группы являются решетками в соответствующих группах Ли.

В теории функций комплексного переменного интегрирование алгебраич. функций и, более общо, решение дифференциальных уравнений с алгебраич. коэффициентами привело к рассмотрению нек-рых специальных функций (названных впоследствии автоморфными функциями), инвариантных относительно различных дискретных групп, состоящих из преобразований вида

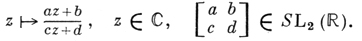  (1)

Некоторые возникающие таким образом Д. п. группы SL₂(ℝ) были рассмотрены примерно в середине 19 в. в работах Ш. Эрмита, Р. Дедекинда (R. Dedekind) и И. Л. Фукса (I. L. Fuchs). Среди них была и группа SL₂(ℤ) (но представленная другим образом, чем у Ж. Лагранжа и К. Гаусса). Обширный класс таких групп, в том числе группа SL₂(ℤ) и нек-рые соизмеримые с ней подгруппы группы SL₂(ℝ), был изучен Ф. Клейном (F. Klein). Почти одновременно, в 1881-82 А. Пуанкаре (Н. Poincaré) дал геометрич. описание всех дискретных групп, состоящих из преобразований вида (1). Эти группы были им названы фуксовыми группами.

В 1-й половине 20 в. рассматривались отдельные классы автоморфных функций многих переменных. Эти функции были связаны с некоторыми арифметически определяемыми Д. п. групп (SL₂(ℝ))^k (модулярные функции Гильберта), Sp_2n(ℝ) (модулярные функции Зигеля) и других полупростых групп Ли.

В кристаллографии начиная с конца 19 в. рассматривались группы симметрии кристаллич. структур, являющиеся не чем иным, как равномерными Д. п. группы движений трехмерного евклидова пространства. Эти и подобные им группы движений n-мерного евклидова пространства - так наз. кристаллографические группы - были изучены с алгебраич. точки зрения Л. Бибербахом (L. Bieberbach) в 1911. Он доказал, в частности, теорему о том, что всякая кристаллографич. группа содержит равномерную Д. п. группы параллельных переносов.

Все эти исследования послужили исходным материалом для общей теории Д. п. групп Ли, основы к-рой были заложены в 50-60-е гг. 20 в.

Построена исчерпывающая теория Д. п. нильпотент-ных групп Ли [9]. Ее основные утверждения: 1) Если Н - унипотентная алгебраич. группа, определенная над ℚ, то группа Н_ℤ ее целых точек является равномерной Д. п. в группе H_ℝ ее действительных точек. (При этом H_ℝ - односвязная нильпотентная группа Ли.) 2) Всякая равномерная Д. п. Г односвязной нильпотентной группы Ли G арифметична в том смысле, что существуют унипотентная алгебраич. группа H, определенная над ℚ, и изоморфизм φ: H_ℝ → G такие, что подгруппа Г соизмерима с φ(H_ℤ). 3) Если Г₁, Г₂ - равномерные Д. п. односвязных нильпотентных групп Ли G₁, G₂ соответственно, то всякий изоморфизм Г₁ → Г₂ однозначно продолжается до изоморфизма G₁ → G₂. 4) Абстрактная группа Г вкладывается в виде равномерной Д. п. в односвязную нильпотентную группу Ли тогда и только тогда, когда Г - конечно порожденная нильпотентная группа без кручения.

Д. п. разрешимых групп Ли изучены достаточно хорошо, но результаты здесь не отличаются таким совершенством, как для нильпотентных групп. Всякая решетка в разрешимой группе Ли является равномерной Д. п. Если Г - решетка в односвязной разрешимой группе Ли G, то группа G допускает точное матричное представление, при к-ром элементы группы Г представляются целочисленными матрицами [13]. Это утверждение можно рассматривать как обобщение теоремы 2) Мальцева. Аналогом теоремы 4) является следующее утверждение. Всякая решетка в односвязной разрешимой группе Ли есть строго полициклическая группа; и обратно, всякая строго полициклич. группа обладает подгруппой конечного индекса, изоморфной решетке в односвязной разрешимой группе Ли.

Наиболее тонкие результаты теории Д. п. групп Ли относятся к Д. п. неразрешимых и, в частности, полупростых групп Ли. В [4] доказана следующая теорема, включающая в себя в виде частных случаев теорему 1) Мальцева, Дирихле теорему о единицах поля алгебраич. чисел и упомянутые выше результаты Зигеля о нек-рых арифметич. Д. п. полупростых групп Ли. Пусть Н - линейная алгебраич. группа, определенная над ℤ. Для того чтобы подгруппа Н_ℤ была решеткой в H_ℝ,

необходимо и достаточно, чтобы группа Н не допускала рациональных гомоморфизмов на группу ℂ*, определенных над ℚ (это условие, в частности, выполняется, если группа Н полупроста или унипотентна). Для того чтобы подгруппа Н_ℤ была равномерной Д. п. в H_ℝ)

необходимо и достаточно, сверх этого, чтобы все унипотентные элементы группы H_ℚ лежали в U_ℚ, где U - унипотентный радикал группы Н.

Аналогом теоремы 2) для Д. п. полупростых групп Ли является следующая теорема арифметичности [11]. Пусть Г - решетка в связной полупростой группе Ли G, не имеющей компактных множителей, и пусть (для удобства формулировки) центр группы G тривиален. Пусть, кроме того, решетка Г неприводима в том смысле, что группа G не может бытьт разложена нетривиальным образом в прямое произведение G₁ × G₂ так, чтобы Г была соизмерима с подгруппой вида Г₁ × Г₂, где Г₁ ⊂ G₁, Г₂ ⊂ G₂. Тогда, если вещественный ранг группы G больше единицы, подгруппа Г арифметична в том смысле, что существуют полупростая алгебраич. группа H, определенная над ℚ, и гомоморфизм φ: H⁰_ℝ → G (где H⁰_ℝ - связная компонента единицы группы H_ℝ) такие, что ядро гомоморфизма φ компактно и подгруппа Г соизмерима с φ(H_ℤ). Предположение о том, что вещественный ранг группы G больше единицы, существенно. Известно, что теорема неверна для группы PSL₂(ℝ) (группы движений плоскости Лобачевского), к-рая вообще играет особую роль в теории Д. п. групп Ли, а также [6], [8] для групп движений пространств Лобачевского размерностей 3, 4 и 5.

Аналогом теоремы 3) для Д. п. полупростых групп Ли является следующая сильная теорема жесткости. Пусть Г₁, Г₂ - неприводимые решетки в связных полупростых группах Ли G₁, G₂, не имеющих компактных множителей, и пусть центры групп G₁, G₂ тривиальны. Тогда если группы G₁, G₂ не изоморфны PSL₂(ℝ), то всякий изоморфизм Г₁ → Г₂ однозначно продолжается до изоморфизма G₁ → G₂ (см. [10], [14]). Исторически доказательству этой теоремы предшествовало доказательство слабой теоремы жесткости [5] о продолжении изоморфизмов, достаточно близких к тождественному (в случае, когда G₁ = G₂). Из слабой теоремы жесткости вытекает, в частности, существование базиса, в к-ром элементы Д. п. записываются алгебраич. числами. Это обстоятельство сыграло важную роль в развитии теории Д. п. полупростых групп Ли.

О Д. п. группы PSL₂(ℝ) см. Фуксова группа.

Из других общих теорем о Д. п. полупростых групп Ли следует отметить теорему плотности Бореля и теорему максимальности Вана. Пусть Г - решетка в связной полупростой группе Ли, не имеющей компактных множителей. Тогда Г плотна в G в топологии Зариского [3] и содержится лишь в конечном числе решеток в группе G [17].

Описание решеток в произвольных группах Ли в известной степени сводится к описанию решеток в полупростых группах Ли благодаря теоремам, аналогичным упомянутой выше теореме Бибербаха о кристаллографич. группах. Говорят, что нормальная подгруппа N группы Ли G обладает свойством Бибербаха, если для любой решетки Г в группе G подгруппа NГ замкнута (и тогда автоматически N ∩ Г - решетка в N, а Г/N ∩ Г - решетка в G/N). Теорема Бибербаха состоит в том, что в группе движений евклидова пространства подгруппа параллельных переносов обладает свойством Бибербаха. Существует обобщение этой теоремы на группы Ли, являющиеся расширением односвязной нильпотентной группы Ли при помощи компактной [1]. Другая теорема такого типа заключается в следующем. Пусть G - связная группа Ли, R - ее радикал, S - максимальная связная полупростая подгруппа, С - максимальная связная компактная нормальная подгруппа группы S; тогда подгруппа RC обладает свойством Бибербаха в G [2]. Известно также, что свойством Бибербаха обладают нильпотентный радикал связной разрешимой группы Ли [12] и коммутант односвязной нильпотентной группы Ли [9].

Топологич. методами (см. Дискретная группа преобразований) доказывается, что всякая равномерная Д. п. связной группы Ли является конечно представимой группой [5]. В действительности всякая решетка в связной группе Ли конечно представима [17], [18].

Лит.: [1] Auslander L., «Аmеr. J. Math.», 1961, v. 83, p. 276-80; [2] его же, там же, 1963, v. 85, р. 145-50; [3] Воrеl А., «Аnn. Math.», 1960, v. 72, p. 179-88; [4] Борель А., Хариш-Чандра, «Математика», 1964, т. 8, № 2, с. 19-71; [5] Вейль А., там же, 1963, т. 7, № 1, с. 3-41; [6] Винберг Э. В., «Матем. сб.», 1967, т. 72, №3. с. 471 -88; [7] Garland Н., Raghunathan М. S., «Аnn. Math.», 1970, v. 92, р. 279-326; [8] Макаров В. С., «Докл. АН СССР», 1966, т. 167, № 1, с. 30-33; [9] Мальцев А. И., «Изв. АН СССР. Сер. матем.», 1949, т. 13, № 1, с. 9-32; [10] Маргулис Г. А., «Успехи матем. наук», 1974, т. 29, № 1, с. 49-98; [11] Маrgulis G. A., Discrete groups of motions of manifolds of non-positive curvature, в кн.: Congrès International des Mathématiques, Vancouver, 1974; [12] Mоstоw G. D., «Ann. Math.», 1954, v. 60, p. 1-27; [13] его же, «Аmеr. J. Math.», 1970, v. 92, p. 1-32; [14] его же, Strong rigidity of locally symmetric spaces, N.Y., 1973; [15] Рагунатан М., Дискретные подгруппы групп Ли, пер. с англ., М., 1977; [16] Сельберг А., «Математика», 1962, т. 6, № 3, с. 3-15; [17] Wang H.-C, «Аmеr. J. Math.», 1967, v. 89, p. 124-32; [18] его же, в кн.: Symmetric Spaces, N. Y., 1972, p. 459-87.

Э. Б. Винберг.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.