
ДИСКРЕТНАЯ ГРУППА
ДИСКРЕТНАЯ ГРУППА преобразований - группа Г гомеоморфизмов хаусдорфова топологич. пространства X, удовлетворяющая следующему условию: для любых точек х, у ∈ Х найдутся такие их окрестности U, V соответственно, что множество
{γ ∈ Г | γ(U) ∩ V ≠ ∅}
конечно. Стабилизатор
Гч = {γ ∈ Г | γ(x) = x}
точки х ∈ X относительно Д. г. преобразований конечен, а орбита любой точки х ∈ Х дискретна. В случае, когда X - метрическое пространство и преобразования из Г являются изометриями, этих двух условий достаточно для того, чтобы группа Г была Д. г. преобразований.
Примеры. 1) Группа параллельных переносов действительной плоскости ℝ2 на всевозможные целочисленные векторы:
(х, у) → (x + n, у + m), где (х, у) ∈ ℝ2; n, m ∈ ℤ.
2) Пусть X - верхняя комплексная полуплоскость
ℂ+ = {z ∈ ℂ | Im z > 0},
рассматриваемая в обычной хаусдорфовой топологии, а Г - группа дробно-линейных преобразований вида
z → (az + b)/(cz + d),
где a, b, с, d - целые числа и ad - bc = 1 (модулярная группа Клейна).
3) Любая конечная группа Г гомеоморфизмов хаусдорфова топологич. пространства X. Если X отделимо, то Г будет собственно разрывной группой преобразований (пример неприводимого алгебраич. многообразия с топологией Зариского показывает, что условие отделимости X является существенным).
4) Скольжений группа произвольного регулярного накрытия р : X → Y, где X - связное и локально линейно связное, а Y- хаусдорфово топологич. пространство, является Д. г. преобразований действующей свободно (т. е. Гx = {1} для любой х ∈ Х), причем само накрытие р совпадает с отображением факторизации по этой группе. Обратно, если Г - свободно действующая Д. г. преобразований связного топологич. пространства X, то факторпространство X/Г хаусдорфово и отображение факторизации р: X → X/Г - регулярное накрытие пространства X/Г с группой скольжения Г. В частности, в силу теоремы униформизации Пуанкаре-Кёбе, всякая риманова поверхность, за несколькими тривиальными исключениями, может быть получена факторизацией верхней комплексной полуплоскости ℂ+ по свободно действующей Д. г. дробно-линейных преобразований с действительными коэффициентами (так наз. фуксовой группе).
5) В теории модулей римановых поверхностей (и, более общо, модулей комплексных многообразий того или иного типа) Д. г. преобразований появляются как модулярные группы. Простейшая из этих групп рассмотрена в примере 2.
6) К числу Д. г. преобразований относятся кристаллографические группы. Весьма широкий класс Д. г. преобразований, включающий фуксовы и кристаллографич. группы, составляют дискретные подгруппы топологич. групп (в частности, групп Ли), рассматриваемые как группы преобразований однородных пространств.
Замкнутое подмножество D топологич. пространства X с Д. г. Г преобразований наз. фундаментальной областью группы Г, если оно является замыканием открытого подмножества и если множества γ(D), где γ ∈ Г, не имеют попарно общих внутренних точек и образуют локально конечное покрытие пространства X. Так, напр., для группы параллельных переносов из примера 1 в качестве фундаментальной области можно взять квадрат
{(x, y) ∈ ℝ2 | 0 ≤ x ≤ 1, 0 ≤ y ≤ 1} (*)
или, более общо, любой параллелограмм с вершинами в целых точках, не имеющий целых точек внутри и на сторонах, а для модулярной группы Клейна (пример 2)) - так наз. модулярную фигуру
D ∈ {z ∈ ℂ+ | -1/2 ≤ Re z ≤ 1/2, |z| ≥ 1}.
Фундаментальная область может быть построена во многих случаях. Напр., если X - полное риманово многообразие, Г - Д. г. преобразований пространства А, состоящая из изометрий этого пространства, и х0 ∈ Х - какая-либо точка, для к-рой стабилизатор Гx0 тривиален, то в качестве фундаментальной области может быть взята область Дирихле
D = {х ∈ X | d(х, х0) d(х, γ(х0)) для всех нетождественных преобразований γ ∈ Г}.
(Здесь через d(х, у) обозначено расстояние между точками х и у из X.) Если X - односвязное полное пространство постоянной кривизны, т. е. сфера, евклидово пространство или пространство Лобачевского, то область Дирихле является выпуклым многогранником.
Построение фундаментальной области и исследование ее свойств доставляют важную информацию о Д. г. преобразований. Так, факторпространство X/Г получается из фундаментальной области путем «склеивания» нек-рых граничных точек. Напр., для группы параллельных переносов (пример 1)) факторпространство получается из квадрата (*) склеиванием противоположных сторон и гомеоморфно двумерному тору. Понятие фундаментальной области лежит в основе комбинаторно-геометрического метода в теории Д. г. преобразований, восходящего к работам А. Пуанкаре по фуксовым [1] и клейновым [2] группам. Этот метод позволяет, с одной стороны, выяснить строение Д. г. преобразований как абстрактной группы (т. е. найти ее образующие и определяющие соотношения) и, с другой стороны, доказать дискретность и найти фундаментальную область группы преобразований с данными образующими. Суть этого метода состоит в следующем. Пусть Г - Д. г. изометрий n-мерного односвязного полного пространства X постоянной кривизны и Ф - выпуклый многогранник, являющийся ее фундаментальной областью. Тогда группа Г порождается множеством
М = {γ ∈ Г | dim (Ф ∩ γ(Ф)) = n - 1}. При этом в качестве определяющих соотношений могут быть взяты всевозможные соотношения следующих двух типов: γ1γ2 = 1, где γ1, γ2 ∈ М и γ1γ2...γk = 1 где γ1, γ2, ..., γk ∈ M,
dim (Ф ∩ γ1(Ф) ∩ γ1γ2(Ф) ∩ ... ∩ γ1γ2 ... γk-1(Ф)) = n - 2,
γiγi+1 ≠ 1 при i = 1, 2, ..., k - 1 и γ1γ2...γi ≠ 1 при l < k (см. [7], [3], [6]). Обратно, пусть Ф - выпуклый многогранник в n-мерном односвязном полном пространстве X постоянной кривизны (не исключается вырожденный случай, когда некоторые двугранные углы многогранника Ф равны π), и для каждой (n-1)-мерной грани F многогранника Ф задана изометрия γF пространства X такая, что Ф ∩ γF(Ф) = F. И пусть: (1) для каждой (n - 1)-мерной грани F многогранника Ф существует такая грань F', что γFγF = 1; (2) для каждой (n - 2)-мерной грани Е многогранника Ф существует такая последовательность F1, F2, ... , Fk его (n-1)-мерных граней, что γF1γF2 ... γFk = 1,
Ф ∩ γF1 (Ф) ∩ γF1γF2 (Ф) ∩ ... ∩ γF1γF2...γFk-1(Ф) = Е
и многогранники Ф, γF1(Ф), γF1γF2 (Ф), ... γF1γF2...γFk-1(Ф) не имеют попарно общих внутренних точек.
Тогда группа изометрий пространства X, порожденная преобразованиями γF, дискретна и многогранник Ф является ее фундаментальной областью. Это вытекает из более общего результата А. Д. Александрова [4] о заполнении пространства выпуклыми многогранниками (см. также [8]). Следующее описание свободно действующих фуксовых групп с компактным факторпространством, принадлежащее А. Пуанкаре (Н. Poincaré), служит примером сказанного выше. При этом считается,
что верхняя комплексная полуплоскость ℂ+ наделена стандартным образом геометрией Лобачевского (модель Пуанкаре плоскости Лобачевского). Фундаментальная область любой из фуксовых групп рассматриваемого типа может быть выбрана в виде выпуклого ограниченного 4g-угольника Ф, обладающего свойствами: а) сумма его внутренних углов равна 2π; б) если при фиксированном направлении обхода границы ∂Ф многоугольника Ф обозначить его стороны через b1, b2, d1, d2, b3, b4, d3, d4, ... ,b2g-1, b2g, d2g-1, d2g, то длина bi равна длине d; при всех i = 1, 2, ... , 2g. На рисунке изображена такая область Дирихле для g = 3. Если при этом обозначить через γi, i = 1, ..., 2g, изометрию плоскости ℂ+, сохраняющую ориентацию и
переводящую с изменением направления bi в di при i четном и di в bi при i нечетном (считается, что стороны Ф имеют направления, индуцированные выбранным направлением обхода ∂Ф), то набор {γ1, γ2, ..., γ2g} является системой образующих группы Г. Единственное соотношение между этими образующими имеет вид
γ1γ2γ-11γ-12 ... γ2g-1γ2gγ-12g-1γ-12g
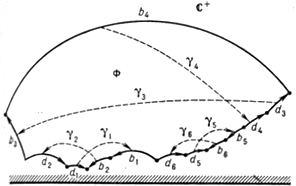
Обратно, если Ф - произвольный выпуклый ограниченный многоугольник, удовлетворяющий условиям а) и б), то группа Г, порожденная изометриями γ1, γ2, ..., γ2g, есть свободно действующая фуксова группа, причем Ф - ее фундаментальная область, а комплексное многообразие ℂ+/Г является компактной римановой поверхностью рода g.
Когомологич. теория Д. г. преобразований состоит в изучении связи между когомологиями пространства X, пространства X/Г и группы Г. В частности (пример 4)) если Г - Д. г. преобразований, являющаяся группой скольжений регулярного накрытия р : X → Х/Г, где X - ациклическое топологич. пространство (т. е. Нn(Х) = 0 при n ≥ 1 и H0(X) = ℤ), то сингулярные когомологии пространства Х/Г и когомологии Г как абстрактной группы с коэффициентами в абелевой группе А (с тривиальной Г-модульной структурой) связаны некоторыми изоморфизмами
Нn(Х/Г, А) ≊ Нn(Г, А), n = 0, 1, ...,
естественными по А (см. [10]). В общем случае связь между упомянутыми выше группами когомологий выражается при помощи некоторых спектральных последовательностей (см. [9], [10]).
См. также Автоморфпая форма, Автоморфная функция, Арифметическая группа.
Лит.: [1] Пуанкаре А., Избр. тр., т. 3, М., 1974, с. 9-62; [2] Pоinсаré Н., «Acta math.», 1883, t. 3, p. 49-92; [3] Gerstenhaber M., «Рrос. Amer. Math. Soc.», 1953; v. 4, p. 745-50; [4] Александров А. Д., «Вестник ЛГУ», 1954, №2, с. 34-43; [5] Coxeter Н. S. М., Моser W. O. J., Generators and relations for discrete groups, В.-Hdlb.-N. Y., 1972; [6] Вейль А., «Математика», 1963, т. 7, №1, с. 3-12; [7] Macbeath A. M., «Ann. Math.», 1964, v. 79, p. 473-88; [8] Abels H., Geometrische Erzeugung von diskontinuierlichen Gruppen, Minister, 1966; [9] Гpотeндик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961; [10] Маклейн С., Гомология, пер. с англ., М., 1966; [11] Lehner J., Discontinuous groups and automorphic functions, Providence, 1964; [12] Сepp Ж.-П., «Математика», 1971, т. 15, № 5, с. 3-6.
Э. Б. Винберг, В. Л. Попов.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'