ДИРИХЛЕ ЯДРО

ДИРИХЛЕ ЯДРО - выражение

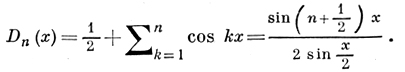
П. Дирихле [1] доказал, что частная сумма S_n(x) ряда Фурье функции f(x) выражается через Д. я.:

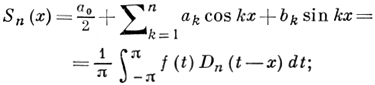
интеграл справа наз. сингулярным интегралом Дирихле.

По аналогии с Д. я. (см. [3]) выражение

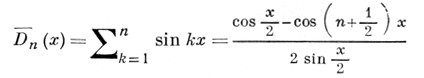
наз. сопряженным ядром Дирихле. Частная сумма ряда, сопряженного к ряду Фурье функции f(х), выражается через сопряженное Д. я.:

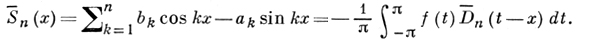
Лит.: [1] Dirichlet P., «J. für Math.», 1829, Bd 4, S. 157-69; [2] его же, Werke, Bd 1, В., 1889; [3] Tauber A., «Monatsh. Math.», 1891, Bd 2, S. 79-118; [4] Бари H. К., Тригонометрические ряды, M., 1961; [5] Зигмунд А., Тригонометрические ряды, т. 1-2, пер. с англ., М., 1965.

Т. П. Лукашенко.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.