ДИРИХЛЕ ХАРАКТЕР

ДИРИХЛЕ ХАРАКТЕР (mod k) - функция χ(n) = = χ(n; k) на множестве целых чисел, удовлетворяющая условиям:

χ(n) ≢ 0,

χ(n) χ(l) = χ(nl),

χ(n) = χ(n + k).

Иными словами, Д. х. (mod к) - это арифметич. функции, к-рые не равны тождественно нулю, вполне мультипликативны и периодичны с периодом k.

Понятие Д. х. ввел П. Дирихле (P. Dirichlet, см. [1]) в связи с изучением закона распределения простых чисел в арифметич. прогрессиях. Он же разработал основы теории Д. х. (см. [2] - [8]), исходя из прямого конструктивного построения их.

Пусть

k = 2αpα11...pαrr

- канонич. разложение k, n - целое взаимно простое с k, (n, k) = 1; С = С0 = 1, если α = 0 или α = 1; С = 2, С0 = 2α-2, если α ≥ 2; С1 = φ(pα11), ..., Сr = φ(pαrr), где

φ - функция Эйлера. Пусть, далее, γ, γ₀, γ₁, ...,γ_r -система индексов числа n по mod k, т. е. система наименьших неотрицательных целых чисел, удовлетворяющих сравнениям

n ≡ (-1)γ5γ0(mod 2α), n ≡ gγjj(mod pαjj), j = 1, ..., r,

где gj - наименьший первообразный корень по mod αjj;

ε, ε₀, ε₁, ..., ε_r - система каких-либо корней из 1 соответственно порядков С, С₀, С₁, ..., С_r. Функция

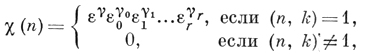
определенная на множестве всех натуральных чисел, наз. характером Дирихле (mod k). Перебирая все возможные значения ε, ε₀, ε₁, ..., ε_r получают

φ(2α)φ(pα11)...φ(αrr) = φ(k)

различных функций χ - Д. х. mod k. Характер с ε = ε₀ = ε₁ = ... = ε_r = 1 наз. главным характером; он обозначается χ₀:

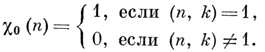
Для любых натуральных чисел n, l и k:

χ(n) x(l) = χ(nl);

χ(n) = χ(l), если n ≡ l(mod k); χ(1) = 1,

χ(n, k) = χ(n; 2α)χ(n, рα11)...χ(n; рαrr);

если χ(n) - Д. х. (mod k), то комплексно сопряженная функция χ(n) - также Д. х. (mod k);

χ^φ(k)(n) = χ₀(n).

Наименьшее из чисел ν, удовлетворяющее равенству χ^ν(n) = χ₀(n) наз. степенью Д. х. Для ν = 1 существует один такой характер χ₀. Если ν = 2, то χ(n) может принимать лишь значения 0; ±1; такие Д. х. наз. действительными, или квадратичными. Если ν ≥ 3, до Д. х. наз. комплексным. χ(n) наз. четным или нечетным соответственно тому, будет χ(-1) = 1 или χ(-1) = -1. Главные свойства сумм Д. х. выражаются формулами

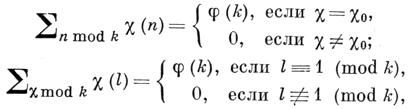
где в 1-й формуле n пробегает полную систему вычетов (mod k), а χ во 2-й формуле - все φ(k) характеров (mod k).

При (l, k) = 1 справедлива формула

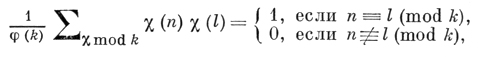
наз. свойством ортогональности Д. х. Она является одной из основных формул Д. х., применяемых в разного рода исследованиях арифметич. прогрессий: kν + l, ν = 0, 1, 2, .... В теории и приложениях Д. х. важны также понятия ведущего модуля характера и примитивного характера. Пусть χ(n; k) -произвольный неглавный характер (mod k). Если для значений n, удовлетворяющих условию (n, k) = 1, число k является наименьшим периодом χ(n; k), то k наз. ведущим, или основным, модулем характера χ, а сам характер χ - примитивным, или первообразным, характером (mod k). В противном случае существуют единственные число k₁ > 1, делящее k, k₁ < k и примитивный характер χ₁(mod k₁) такие, что

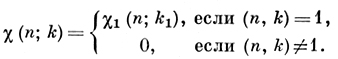
В этом случае χ(n; k) наз. непримитивным, или производным, характером χ(mod d) и говорят, что χ₁ индуцирует χ. Тем самым многие вопросы о характерах сводятся к таковым для примитивных характеров.

Характер χ(n; k) является примитивным тогда и только тогда, когда для любого d, делящего k, d < k, существует а с условиями:

а ≡ 1 (mod d), χ(а; k) ≠ 0; 1.

В аналитич. теории широко используются суммы Гаусса, определяемые для χ(mod k) равенством

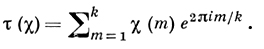
Для примитивного характера χmod k

|τ(x)| = k^1/2. При этом справедливо разложение χ(n) в виде:

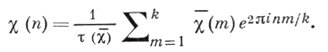
Одной из основных проблем в теории Д. х. является проблема оценки сумм Д. х. χ(mod k), χ ≠ χ⁰:

S(N; M) = ∑_M<n≤N χ(n).

Имеет место оценка Виноградова:

S(N; М) ≪ √k ln k. Установлено [7], что

S(N; M) ≪ k^(r+1)/4r2 (N - M)^1-(1/r) ln k, r = 1, 2, ...,

k - простое число. При M = 1, N = k/2 существует (см. [8]) бесконечная последовательность чисел k, являющихся модулями примитивного действительного характера χ, для к-рой

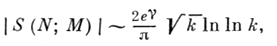
γ - Эйлера постоянная. Это асимптотич. равенство показывает, что предыдущие оценки, вообще говоря, существенно усилить нельзя. Однако существует гипотеза Виноградова, согласно к-рой для любого ε > 0, 1 ≤ М < N,

|S(N; М)| ≪ k^ε(N - М)^1/2.

Доказательство этой гипотезы позволило бы решить ряд крупных проблем теории чисел.

Теория Д. х. лежит в основе теории Дирихле L-функций и является частным случаем общей теории характеров абелевых групп.

Лит.: [1] Дирихле П. Г. Л., Лекции по теории чисел, пер. с нем., М.-Л., 1936; [2] Виноградов И. М., Избр. тр., М., 1952; [3] Карацуба А. А., Основы аналитической теории чисел, М., 1975; [4] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [5] Чудаков Н. Г., Введение в теорию L-функций Дирихле, М., 1947; [6] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [7] Burgess D. А., «Тр. Матем. ин-та», 1973, т. 132, с. 203-205; [8] Лаврик А. Ф., «Изв. АН СССР. Сер. матем.», 1971, т. 35, № 6, с. 1189-207.

А. Ф. Лаврик.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.