ДИРИХЛЕ ТЕОРЕМА

ДИРИХЛЕ ТЕОРЕМА - 1) Д. т. в теории диофантовых приближений: для любого действительного числа α и натурального Q существуют целые а и q, удовлетворяющие условию

|αq - a| < Q^-1, 0 < q ≤ Q.

Дирихле принцип «ящиков» позволяет доказать и более общую теорему: для любых действительных чисел α₁, ..., α_n и натурального Q > 1 существуют такие целые q > 0, a₁, ..., a_n, что

max (|α₁q-a₁|, ..., |α_nq-a_n|) < Q^-1/n, 0 < q ≤ Q.

Лит.: [1] Касселс Дж. В. С., Введение в теорию диофантовых приближений, пер. с англ., М., 1961.

В. И. Берник.

2) Д. т. о единицах - теорема, описывающая структуру мультипликативной группы единиц в порядках полей алгебраич. чисел; получена П. Г. Л. Дирихле (см. [1]).

Каждое поле алгебраич. чисел K степени n над полем рациональных чисел Q имеет n различных изоморфизмов в поле комплексных чисел ℂ. Если при изоморфизме σ : K → ℂ образ поля содержится в поле действительных чисел, то этот изоморфизм наз. вещественным; в противном случае он наз. комплексным. Наряду с каждым комплексным изоморфизмом о имеется сопряженный к нему комплексный изоморфизм σ̅ : K → ℂ, определяемый равенством σ̅(α) = σ̅(̅α̅)̅, α ∈ K. Таким образом число n можно представить в виде n = s + 2t, где s - число вещественных, a 2t - число комплексных изоморфизмов поля К в поле ℂ.

Теорема Дирихле: в произвольном порядке А поля алгебраич. чисел K степени n = s + 2t существует r = s + t - 1 единиц ε₁, ..., ε_r таких, что всякая единица ε ∈ А однозначно представима в виде произведения

ε = ζε₁^s₁...ε_r^s_r,

где s₁, ..., s_r - целые числа, а ζ - некоторый корень из 1, содержащийся в А. Единицы ε₁, ..., ε_r, существование к-рых устанавливается Д. т. наз. основными единицами порядка А. В частности, основные единицы максимального порядка D поля K, совпадающего с кольцом всех целых чисел поля K, наз. обычно основными единицами поля алгебраических чисел K.

Лит.: [1] Dirichlet P. G. L., Werke, Bd 1, В., 1889; [2] Боревич З. И., ШафаревичИ. Р., Теория чисел, 2 изд., М., 1972.

С. А. Степанов.

3) Д. т. о простых числах в арифметической прогрессии: каждая арифметич. прогрессия, первый член и разность которой - натуральные взаимно простые числа, содержит бесконечное число простых чисел. Фактически П. Дирихле доказал (см. [1]), что при любых фиксированных натуральных взаимно простых числах l, k

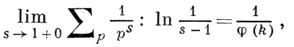
где суммирование ведется по всем простым числам р с условием p ≡ l(mod k), a φ(k) - функция Эйлера. Это соотношение можно интерпретировать как закон равномерного распределения простых чисел по классам вычетов l(mod k), поскольку

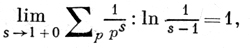
где суммирование ведется по всем простым числам.

Пусть х > 1 - целое, π(х; l, k) - число простых р ≤ х с условием p ≡ l(mod k), где 0 < l < k, l и k - взаимно просты. Тогда

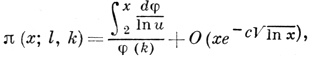
где оценка остаточного члена равномерна по всем k(ln х)^A при любом фиксированном А > 0, с = с(А) > 0 - величина, зависящая только от А (неэффективно). Это современная форма Д. т., непосредственно показывающая характер распределения простых чисел р ≡ l(mod k) в натуральном ряде чисел. Существует предположение (расширенная гипотеза Римана), что при фиксированных взаимно простых l и k и любых целых х > 1

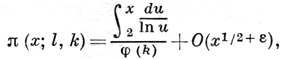
где ε > 0 - произвольно, а О - величина, зависящая от k и ε.

Лит.: [1] Дирихле П. Г. Л., Лекции по теории чисел, пер. с нем., М.-Л., 1936; [2] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [3] Карацуба А. А., Основы аналитической теории чисел, М., 1975.

В. Г. Спринджук.

4) Д. т. о рядах Фурье: если функция f(x) периода 2π кусочно монотонна на отрезке [-π, π] и имеет на нем не более, чем конечное число точек разрыва, т. е. выполнены так называемые условия Дирихле, то ее тригонометрич. ряд Фурье сходится к f(x) в каждой точке непрерывности и к [f(x + 0) + f(x - 0)]/2 в каждой точке разрыва. Доказана впервые П. Дирихле [1]. На функции ограниченной вариации Д. т. обобщил К. Жордан [3].

Лит.: [1] Dirichlet P. G. L., «J. Math.», 1829, Bd 4, S. 157-69; [2] его же, Werke, Bd 1, В., 1889; [3] Jordan С., «С. r. Acad. sci.», 1881, t. 92, № 5, p. 228-30; [4] Бари H. К., Тригонометрические ряды, М., 1961; [5] Зигмунд А., Тригонометрические ряды, пер. с англ., 2 изд., М., 1965.

Т. П. Лукашенко.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.