ДИРИХЛЕ РЯД

ДИРИХЛЕ РЯД - функциональный ряд вида где а_n - комплексные коэффициенты; λ_n, 0 < |λ_n| ↑ ∞, - показатели Д. p., s = σ + it - комплексное переменное. При λ_n = ln n получается так наз. обыкновенный ряд Дирихле

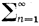  a_n/n^s.

Ряд

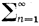  1/n^s

представляет для σ > 1 дзета-функцию Римана. Ряды L(s) = 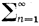χ(n)/n^s,

где χ(n) - функция, наз. Дирихле характером, изучались П. Дирихле (см. Дирихле L-функция). Ряды (1) с произвольными показателями λ_n наз. общими рядами Дирихле.

Общие ряды Дирихле с положительными показателями. Пусть сначала λ_n - положительные числа. Имеет место аналог Абеля теоремы для степенных рядов: если ряд (1) сходится в точке s₀ = σ₀ +it₀, то он сходится в полуплоскости σ > σ₀, причем внутри любого угла |arg(s - s₀)| < φ₀ < π/2 сходится равномерно. Открытая область сходимости ряда есть нек-рая полуплоскость σ > с. Число с наз. абсциссой сходимости Д. р., прямая σ = с - прямой сходимости Д. р., полуплоскость σ > с - полуплоскостью сходимости Д. р. Наряду с полуплоскостью сходимости рассматривается полуплоскость абсолютной сходимости Д. р.: σ > а - открытая область, в к-рой ряд сходится абсолютно (при этом а -абсцисса абсолютной сходимости). Абсциссы сходимости и абсолютной сходимости, вообще говоря, различны; всегда

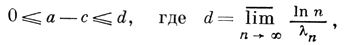
причем имеются Д. p., для к-рых а - c = d. В случае d = 0 для вычисления абсциссы сходимости (абсциссы абсолютной сходимости) имеется формула

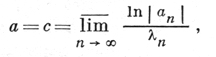
представляющая собой аналог формулы Коши-Адамара. Случай d > 0 сложнее: если величина

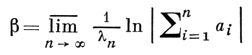
положительна, то с = β; если β ≤ 0 и ряд (1) в точке s = 0 расходится, то с = 0; если β ≤ 0 и ряд (1) в точке s = 0 сходится, то

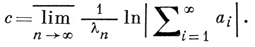
Сумма ряда F(s) в полуплоскости сходимости есть аналитич. функция. При σ → +∞ функция F(σ) ведет себя асимптотически как первый член ряда: а₁е^-λ₁σ (если а₁ ≠ 0). Если сумма ряда равна нулю, то и все коэффициенты ряда равны нулю. Максимальная полуплоскость σ > h, в к-рой F(s) является аналитич. функцией, наз. полуплоскостью голоморфности функции F(s), прямая σ = h наз. прямой голоморфности. Справедливо неравенство h ≤ с, причем возможны случаи, когда h < с. Пусть q - нижняя грань таких чисел β, что в полуплоскости σ > β функция F(s) по модулю ограничена (q ≤ a). Имеет место формула

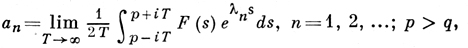
из к-рой вытекают неравенства

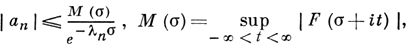
представляющие собой аналог неравенств Коши для коэффициентов степенного ряда.

Сумма Д. р. не может быть произвольной функцией, аналитической в какой-либо полуплоскости σ > h: она, напр., должна стремиться к нулю при σ → +∞. Однако имеет место следующий факт: какова бы ни была функция φ(s), аналитическая в полуплоскости σ > h, найдется такой Д. р. (1), что его сумма F(s) будет отличаться от φ(s) на целую функцию.

Если последовательность показателей имеет плотность

τ = lim_n→∞ < ∞,

то разность между абсциссой сходимости (абсциссы сходимости и абсолютной сходимости совпадают) и абсциссой голоморфности не превосходит величины

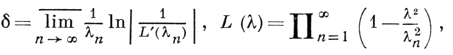
причем имеются ряды, для к-рых эта разность равна δ. Величина δ может быть любой из [0, ∞]; в частности, если λ_n+1 - λ_n ≥ q > 0, n = 1, 2, ..., то δ = 0. Прямая голоморфности обладает тем свойством, что на ней r любом отрезке длины 2πτ у суммы ряда имеется хотя бы одна особенность.

Если Д. р. (1) сходится во всей плоскости, то его сумма F(s) есть целая функция. Пусть

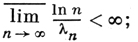
R-порядком целой функции F(s) (порядком по Ритту) наз. величина

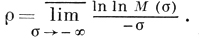
Через коэффициенты ряда она выражается по формуле

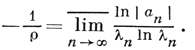
Можно также ввести понятие R-типа функции F(s). Если

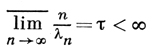
и если в горизонтальной полосе ширины, большей 2πτ, функция F(s) по модулю ограничена, то F(s) = 0 (аналог Лиувилля теоремы).

Ряды Дирихле с комплексными показателями. У Д. р.

F(s) = X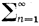 a_ne^-λ_ns (2)

с комплексными показателями 0 < |λ₁| ≤ |λ₂| ≤ ..., открытая область абсолютной сходимости выпукла. Если

lim_n→∞ ln n/λ_n = 0,

то открытые области сходимости и абсолютной сходимости совпадают. Сумма F(s) ряда (2) в области сходимости есть аналитич. функция. Область регулярности функции F(s), вообще говоря, шире области сходимости Д. р. (2). При условии

lim_n→∞ n/λ_n = 0

область регулярности выпукла. Пусть

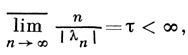
L(λ) - какая-нибудь целая функция экспоненциального типа, к-рая в точках λ_n, n ≥ 1, имеет простые нули, γ(t) - функция, ассоциированная по Борелю с L(λ) (см. Бореля преобразование), D - наименьшее выпуклое замкнутое множество, содержащее все особенности функции γ(t), и

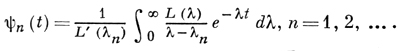
Тогда функции ψ_n(t) регулярны вне D̅, ψ_n(∞) = 0, и они обладают свойством биортогональности к системе {е^λ_ns}: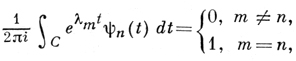

тде С - замкнутый контур, охватывающий D. В том случае, когда ψ_n(t) непрерывны вплоть до границы области D̅, в качестве С можно взять границу ∂D̅. Произвольной функции F(s), аналитической в D (открытой части области D̅) и непрерывной в D̅, отнесем ряд

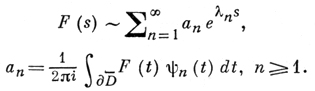  (3)

Для данной конечной выпуклой области D можно построить такую целую функцию L(λ) с простыми нулями λ₁, λ₂ ..., что для любой функции F(s), аналитической в D и непрерывной в D̅, ряд (3) равномерно сходится внутри D и сходится к F(s). Для функции φ(s), аналитической в D (не обязательно непрерывной в D̅), можно найти целую функцию нулевого экспоненциального типа

M(λ) = 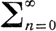c_nλⁿ

и функцию F(s), аналитическую в D и непрерывную в D̅, такие, что

φ(s) = M(D)F(s) = 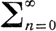c_nF⁽ⁿ⁾(s).

Тогда

φ(s) = 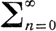а_n М(λ_n) e^λ_ns, s ∈ D.

Представление произвольных аналитич. функций Д. р. в области D установлено также в случаях, когда D - вся плоскость или D - выпуклая бесконечная многоугольная область (ограниченная конечным числом прямолинейных отрезков).

Лит.: [1] Леонтьев А. Ф., Ряды экспонент, М., 1976; [2] Мандельбройт С., Ряды Дирихле, принципы и методы, пер. с англ., М., 1973.

А. Ф. Леонтьев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.