ДИРИХЛЕ РАСПРЕДЕЛЕНИЕ

ДИРИХЛЕ РАСПРЕДЕЛЕНИЕ - распределение вероятностей в симплексе

S_k = {(x₁, ..., x_k): x₁ ≥ 0, ..., x_k ≥ 0, x₁ + ... + x_k = 1},

k = 2, 3, ..., определяемое плотностью вероятности

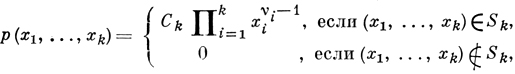
причем ν₁ > 0, ..., ν_k > 0 и

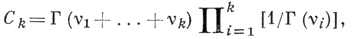
где Г(⋅) - гамма-функция. Частный случай Д. р. -бета-распределение - возникает при k = 2. Д. р. играет важную роль в теории порядковых статистик. Напр., если Х₁, ..., Х_n - независимые случайные величины, подчиняющиеся равномерному распределению на отрезке [0, 1], и Х⁽¹⁾ ≤ ... ≤ X⁽ⁿ⁾ - соответствующий вариационный ряд, то совместное распределение к разностей вида

X^(m₁), X^(m₂) - X^(m₁), ..., X^(m_k-1) - X^(m_k-2), 1 - X^(m_k)

(предполагается, что 1 ≤ m₁ < m₂ < ... < m_k-1) подчиняется Д. р., причем ν₁ = m₁, ν₂ = m₂ - m₁, ..., ν_k-1 = m_k-1 - m_k-2, ν_k = n - m_k-1.

Лит.: [1] Уилкс С., Математическая статистика, пер. с англ., М., 1967, с. 192-96.

Л. Н. Большев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.