ДИРИХЛЕ ИНТЕГРАЛ

ДИРИХЛЕ ИНТЕГРАЛ - функционал, связанный с решением Дирихле задачи для уравнения Лапласа вариационным методам. Пусть Ω - ограниченная область в R_n с границей Г класса С¹, х = (х₁, ..., х_n), а функция u(x) ∈ W¹₂(Ω) (см. Соболева пространство). Д. и. для функции u(х) наз. выражение

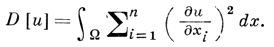
Для некоторой заданной на Г функции φ(х) рассматривается множество π_φ функций из W¹₂(Ω), к-рые удовлетворяют граничному условию u|_x∈Г = φ. Если множество π_φ не пусто, то существует единственная функция u₀(x) ∈ π_φ, для которой

D[u₀] = inf_u∈πφ D[u],

и эта функция является гармонической в области Ω. Верно и обратное утверждение: если гармонич. функция u₀(х) принадлежит множеству π_φ, то на ней достигается inf D[u]. Таким образом, u₀(х) является обобщенным из W¹₂(Ω) решением задачи Дирихле для уравнения Лапласа. Однако не для всякой функции φ можно найти такую функцию u₀(х). Существуют даже непрерывные на Г функции, для к-рых множество π_φ пусто, т. е. в пространстве W¹₂(Ω) не существует ни одной функции u(х), удовлетворяющей условию u|_x∈Г = φ. Классич. решение задачи Дирихле для уравнения Лапласа с такой граничной функцией φ не может иметь конечного Д. и. и не является обобщенным решением из пространства W¹₂(Ω).

Лит.: [1] Михайлов В. П., Дифференциальные уравнения в частных производных, М., 1976.

А. К. Гущин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.