
ДИРИХЛЕ ЗАДАЧА
ДИРИХЛЕ ЗАДАЧА - задача отыскания регулярной в области D гармонич. функции u, к-рая на границе Г области D совпадает с наперед заданной непрерывной функцией φ. Задачу отыскания регулярного в области решения эллиптич. уравнения 2-го порядка, принимающего наперед заданные значения на границе области, также наз. Д. з., или первой краевой задачей. Вопросы, связанные с этой задачей, рассматривались еще К. Гауссом (С. Gauss, 1840), а затем П. Дирихле [1].
Для областей D с достаточно гладкой границей Г решение u(х) Д. з. можно представить интегральной формулой
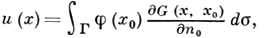 (1)
(1)
где ∂G(x, х0)/∂n0 - производная по направлению внутренней нормали в точке х0 ∈ Г Грина функции G(x, х0), характеризуемой следующими свойствами:
1) G(x, x0) = s-1nr2-n + γ(x, x0) при n ≥ 3
или
G(x, x0) = 1/2π ln (1/r) - +γ(х, х0) при n = 2,
где r = |х - х0| - расстояние между точками х и х0, sn - площадь единичной сферы в ℝn, γ(х, х0) - регулярная в D гармонич. функция как относительно координат х, так и относительно координат х0;
2) G(x, х0) = 0, когда x0 ∈ D, х ∈ Г.
Для шара, полупространства и нек-рых других простейших областей функция Грина строится явно и формула (1) дает эффективное решение Д. з. Получаемые при этом для шара и полупространства формулы носят название Пуассона формул.
Д. з. является одной из основных проблем потенциала теории. Она служила и служит как бы пробным камнем для разрабатываемых новых методов, к-рые затем, в той или иной мере, становятся достоянием общей теории уравнений с частными производными.
Для исследования Д. з. применяются следующие методы.
Вариационный метод основан на том, что среди всех функций u, заданных в D и принимающих наперед заданные значения на Г, минимизирует Дирихле интеграл
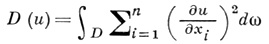
- гармоническая функция. Для D(u) строится специальная минимизирующая последовательность и доказывается сходимость этой последовательности. Поскольку от искомого решения и Д. з. требуется, чтобы существовал интеграл D(u), то вариационный метод применим лишь для таких функций φ, к-рые являются следами на Г функций F, заданных в D̅, и таких, что D(F) существует и ограничен.
В методе потенциалов решение Д. з. ищется в виде потенциала двойного слоя с неизвестной плотностью, определенной на Г. При помощи формул скачка относительно этой плотности получается интегральное уравнение Фредгольма, из к-рого следует существование решения Д. з. с учетом того, что единственность этого решения следует из принципа максимума. Предполагается, что Г ∈ A(1,λ).
В альтернирующем методе Шварца рассматриваются две области D1 и D2 с непустым пересечением D0 такие, что для D1 и D2 в отдельности известен способ решения Д. з. Затем строится процесс, позволяющий найти решение Д. з. для области D = D1 ∪ D2. Границы Г1 и Г2 областей D1 и D2 предполагаются кусочно гладкими, причем во всех точках пересечения Г1 с Г2 как Г1 так и Г2 являются гладкими и пересекаются под ненулевым углом. Строятся последовательности регулярных в областях D1 и D2 гармонич. функций, удовлетворяющих специальным граничным условиям. Затем доказывается, что эти последовательности равномерно сходятся и в D0 их пределы совпадают. Предельная гармонич. функция регулярна в D и является искомым решением Д. з. Метод Шварца можно применять для объединения или пересечения любого конечного числа областей.
Метод выметания в той форме, в к-рой он первоначально был введен А. Пуанкаре (Н. Poincaré, 1890), применяется к таким областям, к-рые допускают исчерпание счетным множеством шаров. Исходным в этом методе является построение ньютонова потенциала, принимающего на границе Г заданные значения φ, а задача затем сводится к замене этого потенциала потенциалом масс, расположенных на Г, без изменения значений φ на Г, т. е. к выметанию масс. При помощи формулы Пуассона такой процесс выметания для шара D легко осуществить в явном виде. Счетное число выметаний из шаров, объединение к-рых исчерпывает область D общего вида, приводит к нек-рому потенциалу масс, расположенных на границе Г, к-рый и дает решение Д. з.
Близким к методу выметания является Перрона метод (или метод верхних и нижних функций), применимый к областям D весьма общего вида. В этом методе строятся последовательности верхних (супергармонических) и нижних (субгармонических) функций, общим пределом к-рых является искомое решение Д. з. Для того чтобы это решение принимало заданное значение в точке Q ∈ Г, необходимо и достаточно существование локального барьера ωQ. Функция ωQ непрерывна, супергармонична в пересечении D̅ ∩ Σ (Σ -шар с центром в точке Q); ωQ > 0 всюду в D̅ ∩ Σ, кроме точки Q, где она обращается в нуль.
Точки Г, для к-рых существует локальный барьер, наз. регулярными точками. Если Г состоит только из регулярных точек, то полученное решение Д. з. непрерывно в D и принимает заданные значения на Г. Однако на Г могут существовать и иррегулярные точки. Напр., в ℝ2 иррегулярными являются изолированные точки Г, а в ℝ3 иррегулярной будет вершина достаточно тонкого острия, входящего внутрь D. Наличие иррегулярных точек приводит к тому, что Д. з. не является разрешимой для всех непрерывных на Г функций φ, либо же решение является неустойчивым по отношению к изменению граничных данных (см. [6]).
Обобщенное решение Д. з., введенное Н. Винером (N. Wiener, 1924), удовлетворяет условиям: а) оно применимо для любых областей; б) оно приводит к классич. решению Д. з., если таковое существует. Пусть область D - предел монотонно возрастающей последовательности регулярных областей {Dn} такой, что Dn ⊂ Dn+1 ⊂ D, и любой компакт K ⊂ D содержится в Dn при n > n(К). Обобщенное решение Д. з. и получается как предел последовательности {un} решений Д. з. для областей Dn и непрерывно продолженной граничной функции φ внутрь D. Решение u не зависит ни от выбора исчерпывающей последовательности {Dn}, ни от способа непрерывного продолжения φ внутрь D.
Имеется трактовка обобщенного решения Д. з. на основе метода Перрона. Пусть Н̅φ - нижняя огибающая семейства всех верхних супергармонич. функций v, удовлетворяющих на Г условию
lim inf v(х) ≥ φ(х0), x ∈ D, х → х0; H̲φ = H̅-φ.
Для любых области D и функции φ имеет место неравенство H̲φ ≤ H̅φ. В случае равенства H̲φ = H̅ = u эта функция u является гармонической. Она наз. обобщенным решением Д. з., а граничная функция φ - разрешимой. Любая непрерывная функция φ разрешима, поведение же обобщенного решения и в точке х0 ∈ Г определяется регулярностью или иррегулярностью х0.
Для обобщенного по Винеру решения Д. з. справедливо интегральное представление в виде формулы Балле Пуссена
u(x) = ∏Г φ(x0) dω(х, D | х0), (2)
являющейся обобщением формулы (1). Здесь dω(x, Е) -гармонич. мера множества E ⊂ Г в точке х0 (см. [5]).
Отсюда возникает возможность рассмотрения обобщенной Д. з. для произвольных граничных функций φ, при этом можно требовать удовлетворения граничного условия лишь в нек-рой ослабленной форме. Напр., если D - область ℝ2 с достаточно гладкой границей Г, а граничная функция φ имеет только точки разрыва 1-го рода, то можно требовать удовлетворения граничного условия лишь в точках непрерывности φ, для обеспечения единственности решения в точках разрыва требуется ограниченность решения. В постановке Н. Н. Лузина обобщенная Д. з. ставится для произвольной измеримой и конечной почти всюду на Г граничной функции φ. Граничное условие может состоять в том, чтобы граничные значения решения по нормали к Г существовали и совпадали с φ почти всюду на Г.
Для общего эллиптич. уравнения 2-го порядка
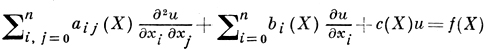 (3)
(3)
Д. з. фредгольмова. При этом ищется регулярное в области решение, принимающее на границе наперед заданные значения. Приведенные выше методы исследования Д. з. для гармонич. функций обобщаются и на уравнение (3).
Для равномерно эллиптич. систем Д. з. может оказаться не только нефредгольмовой, но даже иметь бесконечно много линейно независимых решений (см. [8]).
Д. з. рассматривается и для нек-рых неэллиптич. уравнений или вырождающихся уравнений. В этих случаях Д. з. иногда оказывается некорректной.
Лит.: [1] Diriсhlеt P. G. L., «Abh. der Küniglich. Preus. Acad. der Wiss.», 1850, S. 99-116; [2] Mиpандa K., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [3] Курант Р., Принцип Дирихле, конформные отображения и минимальные поверхности, пер. с англ., М., 1953; [4] его же, Уравнения с частными производными, пер. с англ., М., 1964; [5] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964; [6] Келдыш М. В., «Успехи матем. наук», 1941, в. 8, с. 171-292; [7] его же, «Докл. АН СССР», 1951, т. 77, с. 181-83; [8] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966.
А. Янушаускас.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'