ДИРИХЛЕ ВАРИАЦИОННАЯ ЗАДАЧА

ДИРИХЛЕ ВАРИАЦИОННАЯ ЗАДАЧА - задача отыскания минимума Дирихле интеграла

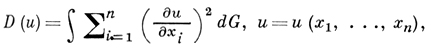
при заданных граничных условиях u|_∂G = φ, где функция φ задана на границе ∂G n-мерной области G. Решение этой задачи является и решением первой краевой задачи для уравнения Лапласа:

Δu = 0, u|_∂G = φ.

Д. в. з. - первая задача на минимизацию функционала, к к-рой было сведено решение краевой задачи для дифференциального уравнения с частными производными.

Д. в. з. естественно рассматривать в классе функций, имеющих первые обобщенные производные, суммируемые с квадратом. В случае ограниченной области это множество функций совпадает с Соболева пространством W¹₂(G), и потому обладает свойством полноты в соответствующей метрике. Кроме того, каждая функция этого пространства имеет на ∂G граничные значения в смысле сходимости почти всюду, к-рые в случае достаточной гладкости границы совпадают с граничными значениями в смысле сходимости в среднем или в смысле предела граничных значений непрерывных в замкнутой области функций, аппроксимирующих в метрике пространства W¹₂(G) заданную функцию. Если G - ограниченная область и если существует хоть одна функция и, для к-рой |D(u)| < ∞ и u|_∂G = φ (такие функции наз. допустимым и), то решение u₀ Д. в. з. существует и единственно. Это решение u₀ является гармонической в G функцией (см. Дирихле принцип). Если граница ∂G области G гладкая, то для того чтобы класс допустимых функций был не пуст, необходимо и достаточно, чтобы φ ∈ B^½₂(∂G). Решение u₀ Д. в. з. может быть найдено прямым вариационным методом. Эти результаты обобщаются как на случай квадратичных эллиптич. функционалов, содержащих производные высших порядков, так и на случай неограниченных областей.

Лит.: [1] Курант Р., Гильберт Д., Методы математической физики, пер. с нем., т. 2, 2 изд., М.- Л., 1951; [2] Соболев С. Л., Некоторые применения функционального анализа к математической физике, Новосиб., 1962; [3] Никольский С. М., «Матем. сб.», 1954, т. 35, № 2, с. 247-66; [4] Кудрявцев Л. Д., «Тр. Матем. ин-та АН СССР», 1959, т. 55, с. 1 - 181.

Л. Д. Кудрявцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.