
ДИРАКА УРАВНЕНИЕ
ДИРАКА УРАВНЕНИЕ - релятивистское волновое уравнение, играющее фундаментальную роль в релятивистской квантовой механике и квантовой теории поля. Д. у. применяется для описания частиц со спином 1/2 (в единицах ℏ), то есть электронов, нейтрино, мюонов, протонов, нейтронов и др., а также позитронов и всех др. античастиц и гипотетических субчастиц - кварков. Д. у. является основой теории частиц полуцелого спина (1/2, 3/2, 5/2 и т. д.), то есть фермионов, к-рые подчиняются Ферми статистике. Напр., обобщением Д. у. для частиц спина 3/2 является Рарита-Швингера уравнение.
Д. у. есть система четырех линейных однородных дифференциальных уравнений с частными производными 1-го порядка с постоянными комплексными коэффициентами, инвариантная относительно общей группы преобразований Лоренца:
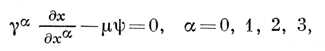
где μ = mc/ℏ, m - масса покоя, хα = х0, х1, х2, x3 ∈ R4 с псевдоевклидовой метрикой (х, y) = ηαβdxαdyβ, а
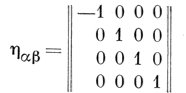
- метрический тензор пространства Минковского с сигнатурой +2; ψ - Дирака спинор (биспинор):
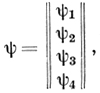
γα = γ0, γ1, γ2, γ3 - Дирака матрицы.
При преобразованиях переменных из общей группы Лоренца - Пуанкаре х'α = L(хα) (см. [2]) биспинор ψ преобразуется по формуле ψ'(х') = S(L)ψ(x), где S(L) - неособенная комплексная матрица размерности 4 × 4. S-матрицы образуют специальное двузначное представление группы L. Д. у. относительно новых переменных ψ'(х'α) не изменяет своего вида (релятивистская инвариантность):
Случай μ = 0 дает уравнение Вейля, описывающее нейтрино. При этом Д. у. разбивается на два независимых уравнения для спинорных функций (спиноров Ван дер Вардена) φ = (ψ1, ψ2) и χ = (ψ3, ψ4). Каждое из них будет не инвариантным относительно отражений (теория с несохранением четности).
Любое решение Д. у. удовлетворяет Клейна-Гордона уравнению, описывающему бесспиновые скалярные частицы
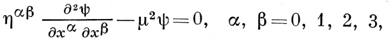
но не всякое решение этого уравнения удовлетворяет Д. у., к-рое получается факторизацией уравнения Клейна-Гордона.
Из Д. у. следует факт наличия у электрона собственного механического спинового момента ℏ/2. Д. у. полностью описывает движение атомных электронов в поле ядра и в других электромагнитных полях, а также взаимодействие электрона с известными элементарными частицами.
Любое релятивистски инвариантное уравнение можно представить в форме Д. у.:
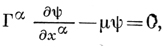
где Гα - обобщение γα. Для уравнения Клейна-Гордона функция ψ имеет 5 компонент, а Гα - 4 пятирядные матрицы, удовлетворяющие соотношениям
ГμГνГρ + ГρГνГμ = ημνГρ + ηρνГμ, Гα = ηαβГβ
(Дуффина-Кеммера матрицы).
Подобно тому как взаимодействие фермионов с электромагнитным полем учитывается в Д. у. заменой производной ∂/∂xα на компенсирующую производную ∂/∂xα - iAα (Аα - 4-потенциал электромагнитного поля), учет взаимодействия фермионов с гравитационным полем в соответствии с общей теорией относительности приводит к обобщению Д. у. на риманово пространство введением соответствующей компенсирующей (ковариантной) производной (см. [3]):
γα(∂/∂xα - Cα)ψ - μψ = 0,
где Сα - спинорные коэффициенты связности, определенные сначала с помощью тетрадного формализма, удовлетворяющие соотношениям
∂γβ/∂xα - Гρ;αβγρ + γβCα - Cαγβ = 0,
Гρ;αβγρ - символы Кристоффеля. Общерелятивистское обобщение Д. у. необходимо при исследовании гравитационного коллапса, при описании предсказываемого эффекта рождения частиц в сильных гравитационных полях и др.
В пространстве с кручением в Д. у. возникает нелинейный добавок кубического типа (см. [4]) и оно переходит в нелинейное уравнение
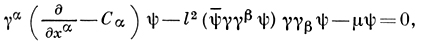
где γ = iγ5, l2 = SπGh/c3, G - гравитационная постоянная.
Уравнение установлено П. Дираком (P. Dirac, 1928).
Лит.: [1] Дирак П. А. М., Принципы квантовой механики, пер. с англ., М., 1960; [2] Боголюбов Н. Н., Щирков Д. В., Введение в теорию квантованных полей, 2 изд., М., 1976; [3] Новейшие проблемы гравитации, пер. с англ., М., 1961; [4] Родичев В. И., «Ж. эксперим. и теор. физ.», 1969, т. 40.
В. Г. Кречет.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'