ДИРАКА МАТРИЦЫ

ДИРАКА МАТРИЦЫ - четыре эрмитовы матрицы α_k, k = 1, 2, 3, и β размера 4 × 4, удовлетворяющие условиям

α_kα_j + α_jα_k = 2δ_kjE, α_kβ + βα_k = 0, α_kα_k = β² = E,

где E - единичная матрица размера 4 × 4. Вместо матриц α_k, β используются также эрмитовы матрицы γ^k = -iβα_k, k = 1, 2, 3, и антиэрмитова матрица γ⁰ = iβ, удовлетворяющие условиям

γ^ϰγ^λ + γ^λγ^ϰ = -2g_ϰλE, ϰ, λ = 0, 1, 2, 3,

где g₀₀ = -g_kk = 1, g^ϰλ = 0 при ϰ ≠ λ, что позволяет записать Дирака уравнение в форме, ковариантной относительно группы преобразований Лоренца. Матрицы α_k, β и γ^ϰ определены с точностью до произвольного унитарного преобразования и представление этих матриц может быть выбрано различными способами. Напр.,

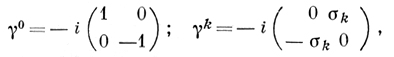
где σ_k- двухрядные Паули матрицы, а 1 и 0 - двухрядные единичная и нулевая матрицы соответственно. С помощью Д. м. можно факторизовать Клейна-Гордона уравнение:

(□ - m²) Eψ = (∑³_ϰ=0 γ^ϰ ∂/∂x^ϰ - mE)(∑³_λ=0 γ^λ ∂/∂x^λ + mE)ψ = 0,

где □ - оператор Д'Аламбера.

Д. м. введены П. Дираком (P. Dirac) в 1928 при выводе уравнения Дирака.

В. Д. Кукин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.