
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ - раздел теории чисел, в к-ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в к-рых некоторым действительным функциям необходимо придать «малые» значения при целочисленных значениях аргументов. В силу этого Д. п. тесно связаны с решением неравенств в целых числах - диофантовых неравенств, а также с решением уравнений в целых числах (см. Диофантовы уравнения).
Если рассматриваемая (аппроксимирующая) функция
F = F(х1, ..., xn)
линейна относительно целочисленных аргументов х1, ..., xn, то Д. п. с функцией F наз. линейными, в противном случае - нелинейными. Если F - однородный многочлен от х1, ..., xn, то Д. п. с функцией F наз. однородными, а если F - неоднородный многочлен, то - не однородными. Иногда рассматривается одновременно несколько функций F, имеющих хотя бы один общий целочисленный аргумент. В этом случае Д. п. наз. совместными. Совместные Д. п. могут быть линейными или нелинейными, однородными или неоднородными в указанном выше смысле.
Численные значения F могут считаться близкими к нулю не обязательно при
|F(х1, ..., xn)| < ε
с некоторым ε > 0, но и при
0 ≤ F (х1, ..., xn) < ε
(односторонние приближения). Функции F могут зависеть от параметров, непрерывно меняющихся в некоторой области,- это параметрич. Д. п. Наконец, область определения и область значений аппроксимирующих функций могут быть не только подмножествами евклидова пространства, а существенно иных топологич. пространств (см. ниже Д. п. в поле р-адиче-ских чисел и Д. п. в поле степенных рядов).
Наиболее старая («простейшая») задача Д. п. - приближения нуля линейной формой αх - у, где α > 0 - фиксированное действительное число, х, у - переменные целые (линейные однородные Д. п.), т. е. задача о рациональных приближениях к а. Для специальных α(α = √2, ∛2, π) эта задача рассматривалась еще в древности (Архимед, Диофант, Евклид), а ее тесная связь с теорией цепных дробей была вполне выяснена Л. Эйлером (L. Euler) и Ж. Лагранжем (J. Lagrange). В частности, если x1 > 0, y1 > 0 таковы, что
|αx1 - у1| = min |αх - у|,
где минимум берется по всем целым х в к.-л. интервале 0 < х ≤ X и по всем целым у, то дробь y1/x1 является подходящей дробью разложения α в цепную дробь. Если неполные частные разложения α в цепную дробь ограничены, то существует С = С(α) > 0 с условием х|αх - у| > С для всех целых x > 0, y > 0. Это верно, напр., для квадратичных иррациональностей α, так как тогда разложение в цепную дробь периодично. С другой стороны, при любом иррациональном α неравенство х|αх - у| < √5 имеет бесконечное число целых решений x > 0, y > 0, а если α = (√5 - 1)/2, то постоянную 1/√5 нельзя заменить меньшим числом. Исследование А. А. Маркова о минимумах неопределенных бинарных квадратичных форм позволило продолжить последнее утверждение: если а не эквивалентно (в смысле теории цепных дробей) (√5 - 1)/2, то неравенство х|ǯх - у| < < 2-3/2 имеет бесконечное число решений; постоянная 2-3/2 не может быть улучшена, если α эквивалентно √2; если α не эквивалентно ни (√5 - 1)/2, ни √2, то неравенство х|αх - у| < 5 (221)-1/2 имеет бесконечное число решений, и т. д. (см. [1]). Постоянные 5-1/2, 2-3/2, 5 (221)-1/2, ... монотонно убывают и имеют предел 1/3.
Приближения нуля линейным неоднородным многочленом αx + у + β (α, β - действительные числа, х, у - переменные целые) - простейший пример линейных неоднородных диофантовых приближений. П. Л. Чебышев доказал, что при любом иррациональном α и любом β неравенство х|αх + у + β| < 2 имеет бесконечное число решений в целых x > 0, у. Постоянная 2 здесь не является наилучшей: Г. Минковский (Н. Minkowski) доказал, что если β ≠ aα + b (а, b - целые), то 2 можно заменить на 1/4, что является наилучшей постоянной. Это утверждение есть следствие доказанного самим Г. Минковским простейшего случая гипотезы о произведении неоднородных линейных форм (см. Минковского гипотеза).
Более сложные задачи общей теории Д. п. касаются аппроксимирующих функций от большего числа целочисленных аргументов (см. Дирихле теорема, Минков-ского теорема, Кронекера теорема). Удобно ввести функцию ||α|| = min |α - n|, где минимум берется по всем целым n (расстояние от α до ближайшего целого). Напр., вместо рассмотренных выше линейных многочленов αх - у и αx + y + β можно брать ||αх|| и ||αx + β|| для целых x > 0. Из теоремы Дирихле следует, что для любых действительных α1, ..., αn существует бесконечное число решений системы неравенств
х1/n max(||α1x||, ..., ||αnx||) < 1
в целых х > 0. Единицу можно заменить меньшим числом (напр., n/(n + 1)), но ни для какого n ≥ 2 наилучшая постоянная неизвестна. Она не может быть сколь угодно малым числом, как показывает пример 1, α1, ..., αn, являющийся базисом действительного алгебраич. поля (см. [1]). Если 1, α1, ..., αn линейно независимы над полем рациональных чисел, то при любых β1, ..., βn и любом ε > 0 существует бесконечное число решений системы неравенств
max (||α1x + β1||, ..., ||αnx + βn||) < ε
в целых x > 0 (теорема Кронекера). Существенная особенность этой теоремы о совместных неоднородных Д. п. состоит в том, что в принципе невозможно (без специальной информации об однородных приближениях к α1, ..., αn) указать скорость убывания ε при возрастании х: для того чтобы линейные формы α1+y1, ..., αn+yn «хорошо» аппроксимировали любые числа β1, ..., βn необходимо и достаточно, чтобы эти формы не могли «хорошо» аппроксимировать специальный набор чисел βi = 0, ..., βn = 0.
Различные на первый взгляд задачи Д. п. иногда оказываются тесно связанными. Напр., принцип переноса Хинчина (см. [1]) связывает разрешимость неравенства
||α1x + ... + αnxn|| < Х-n-λ,
X = max1≤i≤n |x| ≠ 0 (1)
в целых числах х1, ..., xn с разрешимостью системы
max (||α1x||, ..., ||αnx||) < х-(1+μ)/n (2)
в целых x > 0, и обратно: если λ1 и μ1 соответственно точные верхние грани тех λ > 0 и μ > 0, для к-рых (1) и (2) имеют бесконечное число решений, то
λ1 ≥ μ1 ≥ [n2 + (n - 1)λ1]-1λ1.
В частности, равенства λ1 = 0 и μ1 = 0 равносильны (тогда α1, ..., αn соответствуют «наихудшей» аппроксимации, так как (1) при λ =0 и (2) при μ = 0 имеют бесконечное число решений какими бы ни были α1, ..., αn). Подобные связи существуют между однородной и неоднородной задачами (см. [1], [5]) и не только в случае линейных Д. п. Если, напр., α1, ..., αn таковы, что при любом ε > 0 для всех целых x > 0
||α1x|| ... ||αnx|| > C1x-1-ε, (3)
где С1 > 0 зависит только от α1, ..., αn и ε, то каковы бы ни были действительные числа β1, ..., βn, при любом ε1 > 0 система неравенств
max(||α1x + β1|| ... ||αnx + βn||) < Х-1/n+ε1
имеет целое решение х с условием 0 < x ≤ X, если X > X0(α1, ..., αn, ε1). Более того, неравенство (3) обеспечивает «сильную» равномерную распределенность дробных долей ({α1, q), ..., {αnq}), где q = 1, 2, ..., Q; число этих дробей, попадающих в систему интервалов I1 × ... × In, каждый из к-рых лежит внутри единичного интервала, равно |I1| ... |In|Q + Q(Qε2), |I| - длина интервала I, ε2 > 0 - произвольно. Выполнение неравенства (3) для всех целых х > 0 равносильно выполнению неравенства
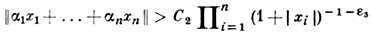
(4)
для всех целых х1, ..., xn ≠ (0) при любом ε3 > 0, где С2 > 0 зависит только от a1, ..., an и ε3.
Доказательство разрешимости или неразрешимости диофантовых неравенств, параметры к-рых определены арифметич. или аналитич. условиями, часто является весьма сложной задачей. Так, задача о приближениях алгебраич. чисел рациональными, систематически изучаемая со времени доказательства неравенства Лиу-вилля (1844) (см. Лиувилля число), до сих пор не получила полного решения (см. Туэ-Зигеля-Рота теорема, Диофантовых приближений проблемы эффекти-визации). Доказано [11], что для алгебраич. чисел α1, ..., αn, вместе с 1 линейно независимых над полем рациональных чисел, выполняются неравенства (3), (4) при любых ε > 0, ε3 > 0. Из этого следует, что система неравенств (1) при любом λ > 0 и система неравенств (2) при любом μ > 0 имеют лишь конечное число решений. Существует тесная связь между подобными теоремами о Д. п. к алгебраич. числам и представлением целых чисел неполными разложимыми формами. В частности, задача о границах для решений х, у диофан-това уравнения Туэ f(x, у) - А при фиксированной целочисленной неприводимой бинарной форме f(x, у) не менее чем 3-й степени и переменном целом А равносильна изучению рациональных приближений к корню α многочлена f(x, 1). Таким путем А. Туэ (А. Thue) доказал конечность числа решений уравнения f(x, y) = A, предварительно получив нетривиальную оценку рациональных приближений к α. Этот подход, обобщенный и развитый К. Зигелем (С. Siegel), привел его к теореме о конечности числа целых точек на алгебраич. кривых рода больше нуля (см. Диофантова геометрия). В. Шмидт [11] использовал подобные идеи для полного решения задачи о представлении чисел разложимыми формами, основываясь на своих аппроксимационных теоремах. В нек-рых случаях связи между теорией Д. п. и теорией диофантовых уравнений не столь непосредственны, хотя законы аппроксимации чисел могут играть главную роль в доказательствах существования решений, асимптотики числа решений и т. п. (задачи типа Варинга проблемы и метод Харди-Литлвуда-Виноградова).
Д. п. к специальным числам, заданным как значения трансцендентных функций в рациональных или алгебраич. точках, изучаются методами теории трансцендентных чисел. Как правило, доказательство иррациональности или трансцендентности к.-л. числа позволяет дать оценку аппроксимации его рациональными пли алгебраич. числами. Для трансцендентного α величину wn(α, H) = min |P(α)|, где минимум берется по всем ненулевым целочисленным многочленам степени не более n и высоты не более Н, наз. мерой трансцендентности числа α. Оценка снизу величины wn(α, Н), главным образом при фиксированном n и переменном Н, составляет содержание многих теорем теории трансцендентных чисел (см. [12]). Напр., К. Малер ([7], [12]) доказал, что
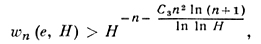
где С3 > 0 - абсолютная постоянная, H > Н0(n). Другим методом А. Бейкер [3] доказал (4) для различных не равных нулю рациональных степеней е с ε3 = C4(ln ln х)-1/2, где
x = mах |xi|, i = 1, 2, ..., n; С4 > 0
зависит только от n, α1, ..., αn. Так как величина wn(α, Н) будет «малой» лишь тогда, когда хотя бы одно алгебраич. число степени не более n и высоты не более Н «близко» к α, то существует связь между оценкой величины wn(α, Н) и оценкой аппроксимации α алгебраич. числами степени не более п. Пусть w*n(α, Н) = min |α - x|, где минимум берется по всем алгебраич. числам ϰ степени не более n и высоты не более Н, и пусть
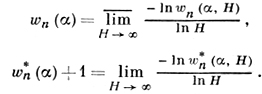
Э. Вирзинг [13] нашел соотношения между величинами wn(α, Н) и w*(α, Н) (α - действительное)
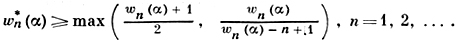
В частности, если wn(α) = n, то w*n(α) = n, и так как wn(α) ≥ n для всех трансцендентных α, то w*n(α) ≥ (n + 1)/2. Из последнего следует, что для всякого трансцендентного α существует бесконечное число алгебраич. ϰ степени не более n, удовлетворяющих неравенству
|α - ϰ| < hϰ-(n+3)/2 + ε4
где hϰ - высота ϰ, ε4 > 0 - произвольно. Э. Вирзинг высказал предположение, что w*n(α) ≥ n для всех трансцендентных α и всех n = 1, 2, .... Кроме очевидного случая n = 1 эта гипотеза доказана для n = 2 (см. [4]). Известно также, что для почти всех (в смысле меры Лебега) действительных α верны равенства
wn(α) = w*n(α) = n, n = 1, 2, ...
(см. [2], Метрическая теория чисел, Диофантовых приближений метрическая теория).
Изучение диофантовых уравнений методами p-адического анализа стимулировало развитие теории Д. п. в поле р-адических чисел Qp, к-рая строится во многом параллельно теории Д. п. в поле действительных чисел, но с учетом неархимедовой топологии поля Qp. Напр., пусть ω ≠ 0 - р-адическое число. Рассматривая приближения нуля (в р-адической метрике) значениями целочисленной линейной формы ωх + у, приходят к рациональным приближениям ω, к-рые, подобно случаю действительных чисел, тесно связаны с разложением ω в цепную (p-адическую) дробь [10]. Справедливы аналоги теорем Дирихле, Кронекера, Минковского и т. п., метрич. теорем, теорем о приближениях алгебраич. числами и т. д. [2], [6], [8]. Диофантовы неравенства в Qp можно интерпретировать как сравнения по «высокой» степени р, что дает иногда возможность получать чисто арифметич. теоремы аналитич. методом. Глубокое развитие Д. п. в поле Qp и его конечных расширениях позволяет использовать метод Туэ-Зигеля-Рота для доказательства теорем об арифметич. структуре чисел, представимых бинарными формами, об оценке дробных долей степеней рациональных чисел и т. п. (см. [10]).
Так как разложение функций в непрерывные дроби осуществляется аналогично разложению чисел в цепные дроби, то естественно возникает дальнейшая аналогия: приближение функций рациональными функциями в метрике поля степенных рядов. Этот подход имеет далекое развитие и приводит к теории Д. п. в поле степенных рядов. Пусть К - произвольное алгебраич. поле, К[х] - кольцо многочленов от х над К, К 〈х-1〉 - поле степенных рядов вида
ω = α-mxm + α-m+1xm-1 + ... + α0 + α1x-1 + ..., αi ∈ K, i = -m, -m + 1, ....
В поле К〈х-1〉 вводится неархимедово нормирование
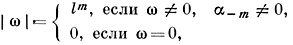
где l > 1 - произвольное фиксированное число. Поле K〈х-1〉 с нормированием |ω| становится метрич. пространством. Изучение «диофантовых» приближений осуществляется по обычной схеме, где K[х] играет роль кольца целых чисел: рассматриваются аппроксимирующие функции со значениями в К〈х-1〉 от конечного числа переменных со значениями в К[х], а близость к нулю оценивается с помощью введенного нормирования. Есть определенное сходство получаемых таким путем результатов со случаем Д. п. в поле действительных чисел, но если К〈х-1〉 заменить полем К〈х〉 рядов вида
α-mx-m + α-m+1x-m+1 + ... + α0 +α1x + ..., αi ∈ K, i = -m, -m + 1, ...,
то результаты будут аналогичны приближениям в поле р-адических чисел (см. [2], [9]).
Д. п. в поле степенных рядов в несколько более конкретной форме (специализации K, явная оценка точности приближения и т. п.) составляют основу нек-рых аналитич. методов теории трансцендентных чисел.
В развитии теории Д. п. выделяются три подхода: глобальный, метрический и индивидуальный. При глобальном подходе изучаются общие законы аппроксимации, справедливые для всех чисел или для всех за «редким» исключением. Сюда относятся теорема Дирихле об однородных приближениях, теорема Кронекера о неоднородных приближениях, общие теоремы о приближении чисел алгебраическими, классификации чисел по аппроксимационным свойствам и т. п. Соответственно применяемые методы носят «глобальный» характер (непрерывные дроби, применения теоремы Минковского и методы геометрии чисел и т. п.). Метрич. подход требует описания аппроксимационных свойств чисел на основе понятий теории меры (см. Диофантовых приближений метрическая теория, Метрическая теория чисел). Получаемые результаты касаются не всех, а почти всех (в смысле определенной меры) чисел из рассматриваемых множеств или описываются с помощью нек-рой метрич. характеристики (размерность Хаусдорфа, емкость и т. п.). Применяемые методы тесно связаны с теорией меры, теорией вероятностей и смежными дисциплинами. Индивидуальный подход касается аппроксимационных свойств специальных чисел (алгебраич. числа, е, π, ln 2 и т. п.) или требует построения чисел с определенными аппроксимационными свойствами (числа Лиувилля, T-числа Малера и т. п.). Методы решения таких задач специфичны и часто создаются специально для анализа конкретной задачи.
Лит.: [1] Касселс Дж. В. С, Введение в теорию диофантовых приближений, пер. с англ., М., 1961; [-2] Спринджук В. Г., Проблема Малера в метрической теории чисел, Минск, 1967; [3] Baker A., «Canad. J. Math.», 1965, v. 17, p. 616-26; [4] Davenport H., Schmidt W., «Acta Arithm.», 1967, v. 13, p. 169-76; [5] Koksma J. F., Diophantische Approximationen, В., 1936; [6] Lutz E., Sur les approximations diophantiennes linéaires p-adiques, P., 1955; [7] Mahler K., «Math. Z.», 1930, Bd 31, S. 729-32; [8] его жe, «Jahresber. DMV», 1934, Bd 44, S. 250-55; [9] его же, «Аnn. Math.», 1941, v. 42, p. 488 - 522; [10] его же, Lectures on Diophantine approximations [s. 1.], pt 1, 1961; [11] Schmidt W., «L'enseignment Math. Revue intern., ser. 2», 1971, v. 17, №3-4, p. 187-253; [12] Schneider Th., Einführung in die transzendenten Zahlen, В., 1957; [13] Wirsing E., «J. reine und angew. Math.», 1961, Bd 206, № 1-2, S. 67-77.
В. Г. Спринджук.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'