ДИНИ ПРИЗНАК

ДИНИ ПРИЗНАК: если 2π-периодическая интегрируемая на отрезке [0, 2π] функция f(x) в точке х₀ удовлетворяет условию

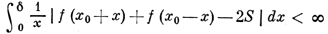
при фиксированном числе S, -∞ < S < +∞, и каком-либо δ > 0, то ряд Фурье функции f(x) в точке х₀ сходится к числу S. Д. п. доказан У. Дини [1]. Его утверждение окончательно в следующем смысле. Если μ(t) ≥ 0 - такая непрерывная функция, что функция μ(t)/t не интегрируема в окрестности точки t = 0, то можно найти непрерывную функцию f(t), ряд Фурье к-рой расходится в точке t = 0, причем

|f(t) - f(0)| ≤ μ(t)

для малых t.

Лит.: [1] Dini U., Serie di Fourier e altre rappresentazioni analitiche delle funzione di una variable reale, Pisa, 1880; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1, М., 1965.

Б. И. Голубов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.