ДИКИЙ УЗЕЛ

ДИКИЙ УЗЕЛ - узел L в евклидовом пространстве Е³ такой, что не существует гомеоморфизма Е³ на себя, при к-ром L переходит в замкнутую ломаную линию, состоящую из конечного числа отрезков.

Рис. 1.

Так, дикими являются узлы, содержащие так наз. дуги Фокса-Артина - некоторые простые дуги, полученные диким вложением в Е³. Напр., для дуги L₁ (рис. 1) фундаментальная группа π₁(E³\L) нетривиальна, для дуги L₂ (рис. 2) группа π₁(Е³\L) тривиальна, но само E³\L не гомеоморфно дополнению в Е³ к точке.

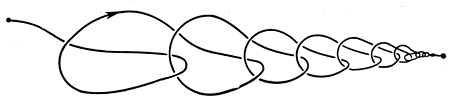
Рис. 2.

Лит. см. при ст. Дикая сфера.

М. И. Войцеховский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.