ДИЗЪЮНКТНЫЕ ЭЛЕМЕНТЫ

ДИЗЪЮНКТНЫЕ ЭЛЕМЕНТЫ, независимые элементы, - элементы х ∈ X и y ∈ Х векторной решетки X, обладающие тем свойством, что

|x| ∧ |y| = 0,

где

|z| = х ∧ (-х),

что равносильно

|z| = sup(x, -х).

Соответственно,

|х| = х ∧ (у),

что равносильно

|x| = inf(x, у).

Символы ∧ и ∨ являются, соответственно, дизъюнкцией и конъюнкцией. Множества A ⊂ X и B ⊂ X наз. дизъюнктными, если дизъюнктна любая пара элементов х ∈ А, у ∈ В. Элемент х ∈ X наз. дизъюнктным множеству A ⊂ X, если дизъюнктны множества {х} и А. Дизъюнктная пара элементов обозначается x ⊥ f или xdy, а дизъюнктная пара множеств - соответственно А ⊥ В или AdB.

Пример Д. э.: положительная x₊ = x ∨ 0 и отрицательная х_- = (-x) ∨ 0 части элемента х.

Если элементы х_i, i = 1, 2, ..., n попарно дизъюнктны, то они линейно независимы; если А и В - Д. э., то порождаемые ими линейные многообразия тоже дизъюнктны; если х_α ⊥ у, α ∈ 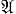, причем

sup_α х_α = х

существует, то x ⊥ y. Для Д. э. упрощается ряд структурных соотношений; напр., если x ⊥ y, то

|х + у| = |x| + |y|,

(х + у) ⋀ z = x ⋀ z + y ⋀ z для z > 0, и т. д.

Понятие Д. э. может быть введено и в более общих частично упорядоченных множествах, напр. в булевых алгебрах.

Лит.: [1] Канторович Л. В., Вулих Б. З., Пинскер А. Г., Функциональный анализ в полуупорядоченных пространствах, М.-Л., 1950; [2] Вулих Б. 3., Введение в теорию полуупорядоченных пространств, М., 1961; [3] Бурбаки Н., Интегрирование. Меры, интегрирование мер, пер. с франц., М., 1967.

В. И. Соболев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.