ДИЗЪЮНКТНЫЕ ПРЕДСТАВЛЕНИЯ

ДИЗЪЮНКТНЫЕ ПРЕДСТАВЛЕНИЯ - унитарные представления π₁, π₂ нек-рой группы или, соответственно, симметричные представления нек-рой алгебры с инволюцией, удовлетворяющие следующим эквивалентным условиям: 1) единственный ограниченный линейный оператор из пространства представления π₁ в пространство представления π₂ равен нулю; 2) любые ненулевые подпредставления представлений π₁ и π₂ не эквивалентны. Понятие Д. п. плодотворно при изучении факторпредставлений; в частности, представление π является факторпредставлением тогда и только тогда, когда я нельзя представить в виде прямой суммы двух ненулевых Д. п. Любые два факторпредставления либо дизъюнктны, либо одно из них эквивалентно подпредставлению другого (и в последнем случае представления квазиэквивалентны). Понятие Д. п. играет важную роль в разложении представлений в прямой интеграл: если π - представление в сепарабельном гильбертовом пространстве Н, 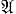- Неймана алгебра в Н, порожденная операторами представления, Z - центр ,

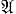H = ∫^⊕ H(l)dμ(l)

- разложение пространства Н в прямой интеграл гильбертовых пространств, соответствующее разложению

π = ∫^⊕π(l)dμ(l),

и если при этом алгебра Z соответствует алгебре диаго-нализуемых операторов, то π(l) является факторпредставлением для почти всех l, и представления π(l) попарно дизъюнктны для почти всех l. Существует простая связь между дизъюнктностью представлений сепарабельной локально компактной группы (соответственно сепарабельной алгебры с инволюцией) и взаимной сингулярностью представителей канонических классов мер на квазиспектре группы (алгебры), соответствующих этим представлениям.

Лит.: [1] Диксмье Ж., С*-алгебры и их представления, пер. с франц., М., 1974.

А. И. Штерн.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.