ДИВИЗОРИАЛЬНЫЙ ИДЕАЛ

ДИВИЗОРИАЛЬНЫЙ ИДЕАЛ - дробный идеал а целостного коммутативного кольца А такой, что а = А : (А : а) (здесь А : а обозначает множество элементов х из поля частных кольца А, для к-рых ха ⊂ А). Иногда Д. и. наз. дивизором кольца. Для любого дробного идеала а идеал а̃ = А : (А : а) дивизориален. Множество D (А) Д. и. кольца А является решеточно упорядоченным коммутативным моноидом (полугруппой), если произведением двух Д. и. а и b считать 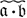, а положительными (или эффективными) считать целые Д. и. a ⊂ A. Моноид D(A) является группой тогда и только тогда, когда кольцо А вполне целозамкнуто; при этом обратным к дивизору а будет А : а.

Обычно Д. и. рассматривают в кольце Крулля (напр., в нётеровом целозамкнутом кольце); в этом случае простые идеалы высоты 1 дивизориальны и образуют базис абелевой группы дивизоров D(A). Этот результат, по существу, был установлен Э. Артином (Е. Artin) и Б. Л. Ван дер Варденом (В. L. Van der Waerden) (см. [1]) в их теории квазиравенства идеалов (идеалы а и b квазиравны, если а̃ = b̃) и завершил одну из центральных тем алгебры того времени - изучение разложения идеалов.

Главные дробные идеалы, а также обратимые дробные идеалы являются дивизориальными и образуют соответственно подгруппы F(A) и J(А) в D(A). Фактор-группы D(A)/F(A) = C(A) и J(A)/F(A) = Pic(A) наз. соответственно классов дивизоров группой и Пикара группой кольца А.

Лит.: [1] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [2] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971.

В. И. Данилов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.