ДИВИЗОР

ДИВИЗОР - обобщение понятия делителя элемента коммутативного кольца. Впервые (под назв. «идеальный делитель») это понятие возникло в работах Э. Куммера [1] об арифметике круговых полей.

Теория Д. для коммутативного кольца А с единицей без делителей нуля состоит в построении гомоморфизма φ из мультипликативной полугруппы А^* ненулевых элементов А в нек-рую полугруппу D₀ с однозначным разложением на множители, элементы к-рой наз. (целыми) дивизорами кольца А. Теория Д. позволяет свести ряд вопросов, связанных с разложением на простые множители в кольце А, где это разложение может быть неоднозначно, к рассмотрению разложения на простые множители в D₀. Образ φ(a) ∈ D₀ элемента а ∈ А^* обозначается (а) и наз. главным дивизором элемента а. Говорят, что а ∈ А^* делится на Д. 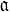∈ D₀, если 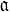делит (а) в D₀.

Точнее, пусть D₀ - свободная абелева полугруппа с единицей, свободные образующие к-рой наз. простыми дивизорами, и пусть задан гомоморфизм φ: A^* → D₀. Гомоморфизм φ определяет теорию Д. кольца А, если он удовлетворяет следующим условиям.

1) Для а, b ∈ А^* элемент а делит b в кольце А тогда и только тогда, когда (а) делит (b) в D₀.

2) Для любого 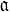∈ D₀

{0, а ∈ А | 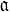делит (а)}

является идеалом кольца А.

3) Если 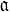, 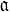' ∈ D₀ и для любого а ∈ А*(а) делится на а тогда и только тогда, когда (а) делится на 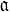', то = '.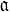

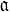Этими условиями гомоморфизм φ, если он существует, определяется однозначно с точностью до изоморфизма. Ядро ker φ совпадает с группой единиц кольца А. Элементы из D₀ наз. положительными Д. кольца А. Пусть K - поле частных кольца А и D ⊃ D₀ - свободная абелева группа, порожденная множеством простых Д. Тогда для любого с ∈ K*, К* = К\0, можно определить главный дивизор (c) ∈ D. Если с = а/b, где а, b ∈ А*, то (с)=(а)/(b). Элементы группы D наз. дробными дивизорами (или просто дивизорами) кольца А (или поля К). Каждый Д. 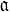∈ D может быть записан в виде

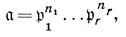
где 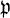_i - простые Д. Либо (в аддитивной записи):

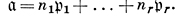
Если а ∈ К* и (a) = ∑n_i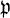i, то отображение а → ∑n_i является дискретным нормированием на поле K, наз. существенным нормированием поля К. Гомоморфизм φ продолжается до гомоморфизма ψ: K* → D, где ψ(с) = (с), содержащегося в точной последовательности

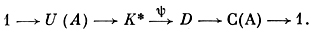
Здесь U(А) - группа единиц кольца А, а группа С(А) наз. группой классов дивизоров кольца А (или поля K). Два Д., принадлежащие одному смежному классу по подгруппе главных Д., наз. эквивалентными (в алгебраической геометрии, где рассматривается целый ряд других эквивалентностей для Д., эта эквивалентность называется линейной).

Теория Д. существует для всякого дедекиндова кольца, в частности, для колец целых элементов в полях алгебраич. чисел, причем в этом случае элементы D₀ находятся во взаимно однозначном соответствии с ненулевыми идеалами кольца А (Д. а при этом соответствует идеал всех элементов А, делящихся на 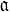). По этой причине в дедекиндовых кольцах группу Д. наз. также группой идеалов, а группу классов Д. - группой классов идеалов.

Группа классов Д. поля алгебраич. чисел конечна, и с вычислением ее порядка (числа классов) и структуры связаны многие задачи алгебраической теории чисел (см. [2]).

Более общо, теория Д. существует для Крулля колец (см. [11]). В этом случае роль D₀ играет полугруппа дивизор иалъных идеалов кольца, а роль D играет группа дробных дивизориальных идеалов.

Обобщением понятия дробного дивизориального идеала коммутативного кольца на случай алгебраич. многообразия или аналитич. пространства служит понятие дивизора Вейля. Так называется целочисленная формальная конечная линейная комбинация ∑n_WW неприводимых замкнутых подпространств W в X коразмерности 1. Дивизор Вейля наз. положительным, или эффективным, если все n_W ≥ 0. Все дивизоры Вейля образуют группу Z¹(X) (группа дивизоров Вейля). В случае, когда X - гладкое алгебраич. многообразие, понятие дивизора Вейля совпадает с понятием алгебраического цикла коразмерности 1.

Если А - нётерово кольцо Крулля, то каждый простой дивизориальный идеал 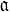в А определяет подпространство V(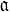) коразмерности 1 в схеме X = Spec(A), а

каждый Д. 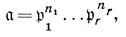может быть отождествлен тем самым с дивизором Вейля ∑n_iV().

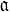Пусть X - нормальная схема, а f - мероморфная функция на X. Каноническим образом определяется главный дивизор Вейля:

(f) = ∑n_WW.

Здесь n_W есть значение дискретного нормирования кольца O_X,W общей точки подмногообразия W на представителе f в O_X,W. Если

(f) = ∑n⁺_WW + ∑n^-_WW,

где n⁺_W > 0, а ^-_W < 0, то дивизор Вейля (f)₀ = ∑n⁺_WW наз. дивизором нулей, a. ∑n^-_WW - дивизором полюсов функции f. Множество главных дивизоров Вейля является подгруппой Z_p(X) группы Z¹(X). Факторгруппа Z¹(X)/Z¹_p(X) обозначается С(Х) и наз. группой классов дивизоров схемы X. Если X = Spec А, где А - нётерово кольцо Крулля, то С(Х) совпадает с группой классов Д. кольца А.

Пусть К - поле алгебраич. функций. Д. поля К наз. иногда формальные конечные целочисленные комбинации дискретных нормирований ранга 1 поля К. Если К есть поле алгебраич. функций от одной переменной, то каждый такой Д. может быть отождествлен с дивизором Вейля его полной неособой модели.

Пусть X - регулярная схема или комплексное многообразие и D = ∑n_WW - дивизор Вейля. Для любой точки х ∈ X существует такая открытая окрестность U, что ограничение D на U

D|_U = ∑n_W(W ∩ U)

является главным Д. (f_U) для нек-рой мероморфной функции f_U на U. Функция f_U определена однозначно с точностью до обратимой функции на U и наз. локальным уравнением Д. D в окрестности U, а соответствие U → f_U определяет сечение пучка M^*_X/^*_X. Вообще, дивизором Картье на окольцованном пространстве (X, _X) называется глобальное сечение пучка M^*_X/^*_X (пучка ростков дивизоров). Здесь М_X обозначает пучок ростков мероморфных (или рациональных) функций на X, т. е. пучок, сопоставляющий каждому открытому U ⊂ X полное кольцо частных кольца Г(U, _X), а М^*_X и ^*_X - пучки обратимых элементов в М_X и _X соответственно. Дивизор Картье можно задавать набором локальных уравнений

f_i ∈ Г(U, M^*_X),

где {U_i} - открытое покрытие X, причем на U_i ∩ U_j функция f_i/f_j должна быть сечением пучка ^*_X. В частности, мероморфная функция f определяет Д. div (f), наз. главным. Множество х ∈ М таких, что (f_i)_x ∉ ^*_X,x, наз. носителем дивизора. Дивизоры Картье образуют абелеву группу Div(Z), а главные Д.- ее подгруппу Div_l(X). Каждый Д. D ∈ Div (X) определяет обратимый пучок _X(D), содержащийся в M_X: если D представлен локальными уравнениями на покрытии {U_i}, то

 _X(D)|_Ui = f^-1_i|_Ui ⊂ M_X|Ui.

Сопоставление D ↦ _X(D) является гомоморфизмом группы Div(X) в Пикара группу Pic(X) = H¹(X, ^*_X). Этот гомоморфизм включается в точную последовательность

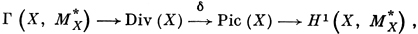
получающуюся из точной последовательности пучков

0 → ^*_X → M^*_X → M^*_X/^*_X → 0.

Таким образом, ker δ = Div_l (X). Если D - D' есть главный Д., то D и D' наз. линейно эквивалентными. Если X - квазипроективное алгебраич. многообразие или комплексное пространство Штейна, то гомоморфизм δ: Div(X) → Pic(X) сюръективен и индуцирует изоморфизм группы классов линейно эквивалентных Д. Div(X)/Div_l(X) на группу Пикара Pic(X).

Если X - комплексное пространство, то вопрос о том, когда данный Д. является главным, есть вторая Кузена проблема. Напр., на комплексном пространстве Штейна (X, ) группа классов Д. тривиальна тогда и только тогда, когда Н²(Х, ℤ) = 0.

Д. D наз. эффективным (или положительным), если _X ⊂ _X(D). В этом случае _X(-D) является пучком идеалов в _X; носитель Д. D со структурным пучком _X/_X(D) образует подпространство в X, обозначаемое также D.

Для нормальной нётеровой схемы или нормального аналитич. пространства X имеется естественный гомоморфизм

cyc: Div(X) → Z¹(X),

переводящий D ∈ Div(X) в ∑n_WW, где n_W = ν_W(f), f - локальное уравнение D в окрестности W, a ν - соответствующее W дискретное нормирование (см. [3]). Гомоморфизм сус инъективен и переводит эффективные Д. в эффективные; сус биективен тогда и только тогда, когда X локально факторнально (напр., когда X - неособая схема или аналитич. многообразие). В случае, когда сус биективен, дивизоры Вейля и Картье отождествляются.

Пусть f : Х' → Х - морфизм схем, плоский в коразмерности 1. Тогда для любого дивизора Картье или Вейля D на X определен его обратный образ f^*(D). При этом сус(f^*(D)) = f^*(сус(D)). Отображение D → f^*(D) является гомоморфизмом групп, переводит главные Д. в главные и тем самым определяет гомоморфизм групп

f^* : Pic(X) → Pic(X')

(соответственно f^* : С(X) → С(X')).

Если X' - открытое множество в X, дополнение к к-рому имеет коразмерность ≥2 и f - вложение X' в X, то f^*: С(Х) → С(Х') - изоморфизм, а f : Pic(X) → Pic(X') является изоморфизмом при условии, что схема X локально факториальна.

Пусть X - гладкое проективное многообразие над ℂ Каждый Д. D на X определяет класс гомологии

[D] ∈ H_{2 dim X - 2}(X, ℤ);

двойственный по Пуанкаре к [D] класс когомологий совпадает с Чжэня классом c₁(_X(D)) ∈ Н²(Х, ℤ) обратимого пучка _X(D). Так на Div(X) возникает гомологич. эквивалентность. Имеется теория пересечения Д. (см. [7]), приводящая к понятию численной эквивалентности, тесно связанной с понятием алгебраич. эквивалентности Д. (см. Алгебраический цикл). Группа

Pic⁰(X) = Div_a(X)/Div_l(X),

где Div_a(X) обозначает группу Д., алгебраически эквивалентных нулю, естественным образом снабжается структурой абелева многообразия (Пикара многообразие; если X - кривая, то оно также наз. Якоби многообразием кривой X). Группа Div(X)/Div_a(X), наз. группой Нерона-Севери, имеет конечное число образующих. Последние два факта верны и для алгебраич. многообразий над произвольным полем.

Если X - одномерное комплексное многообразие (риманова поверхность), то Д. на X можно понимать как конечные линейные комбинации

D = ∑_i k_ix_i,

где k_i ∈ ℤ, x_i ∈ Х. Число ∑k_i наз. степенью Д. D. Для компактной римановой поверхности X рода g группа классов Д. степени 0 есть g-мерное абелево многообразие и совпадает с многообразием Пикара (или с многообразием Якоби). Если f - мероморфная функция на X, то главный Д.

div (f) = ∑_i m_ix_i - ∑_j n_jy_j,

где x_i - нули, y_j - полюсы функции f, а m_i, n_j - их кратности. Тогда ∑_im_i = ∑_jn_j, т. е. главный Д. имеет степень 0. Д. D степени 0 на X является главным тогда и только тогда, когда существует такая сингулярная одномерная цепь С, что

∂C = D и ∫_C ω = 0

для всех голоморфных форм со степени 1 на X (теорема Абеля). См. также Абелев дифференциал.

Лит.: [1] Кummеr Е. Е., «J. reine und angew. Math.», 1847, Bd 35, S. 327-67; [2] Боревич З. И., Шафapeвич И. P., Теория чисел, 2 изд., М., 1972; [3] Вейль А., Введение в теорию кэлеровых многообразий, пер. с франц., М., 1961; [4] Сartier P., «Bull. Soc. math. France», 1958, t. 86, p. 177-251; [5] Grоthendieсk A., «Publ. Math. IHES», 1967, № 32, ch. 4, pt. 4; [6] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [7] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [8] Шевалле К., Введение в теорию алгебраических функций от одной переменной, пер. с англ., М., 1959; [9] Ганнинг Р., Росси Х., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969; [10] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [11] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971; [12] Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960.

В. И. Данилов, Л. В. Кузьмин, А. Л. Онищик.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.