ДИВЕРГЕНЦИЯ

ДИВЕРГЕНЦИЯ, расхождение, векторного поля a(х) в точке (х¹, ... , хⁿ) - скалярная величина

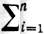 ∂/∂xⁱ aⁱ(x)

где аⁱ(х) - компоненты вектора a(х).

Д. обозначается div a(х) или в виде скалярного произведения (∇, a) Гамильтона оператора ∇ = (∂/∂x¹, ..., ∂/∂xⁿ) на вектор a(х).

Если векторное поле a(х) есть поле скоростей установившегося течения несжимаемой жидкости, то div a(х) совпадает с интенсивностью источников (div a > 0) или стоков (div a < 0) в точке х.

Интеграл

∫_E div (ρa) dx,

где ρ - плотность жидкости, вычисленный для n-мерной области Е, равен количеству жидкости, «расходящейся» в единицу времени из Е. Это количество (см. Остроградского формула) совпадает с величиной

∫_{y&#№8712;∂E} (N(y), ρa((y)) ds = 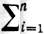∫_∂E N_i(y) ρaⁱ(y) ds,

где N = (N₁, ... , N_n) - единичный вектор внешней нормали к ∂Е, ds - элемент площади ∂Е. Д. div a(х) является производной по объему потока поля a(x) через замкнутую поверхность:

div a(х) = lim (1/объем E) ∫_∂E (N, a) ds при Е → х.

Таким образом, Д. носит инвариантный относительно выбора системы координат характер.

В криволинейных координатах y = (y¹, ..., уⁿ), y^j = y^j(x), 1 ≤ j ≤ n,

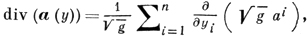
где

g = det(g_ij) g_ij = 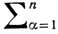∂y_α/∂xⁱ ∂y^α/∂x^j, a = 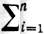aⁱ(y) s_i(y)

а s_i(y) - орт касающийся i-й координатной линии в точке у:

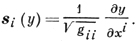
Д. тензорного поля

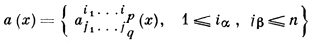
типа (р, q), заданного в области n-мерного аффинного пространства связности, определяется с помощью абсолютных (ковариантных) производных компонент а(х) с последующей сверткой и является тензором типа (р - 1, q) с компонентами

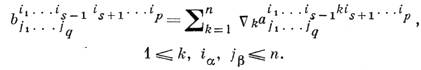
В тензорном анализе и дифференциальной геометрии Д. называется также дифференциальный оператор, действующий в пространстве дифференциальных форм и связанный с оператором внешнего дифференцирования.

Лит.: [1] Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 9 изд., М., 1965; [2] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967.

Л. П. Купцов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.