ДИАДИЧЕСКИЙ БИКОМПАКТ

ДИАДИЧЕСКИЙ БИКОМПАКТ - бикомпакт, являющийся непрерывным образом обобщенного канторова дисконтинуума. Д. б. были введены П. С. Александровым в связи с естественной попыткой обобщить на произвольные бикомпакты теорему о том, что каждый компакт является непрерывным образом канторова множества. Класс Д. б. - наименьший класс бикомпактов, содержащий все метрич. компакты и замкнутый относительно тихоновского произведения и непрерывного отображения. Свойства Д. б. Всякая бикомпактная топологич. группа диадична. Д. б. удовлетворяет Суслина условию и, более того, всякое регулярное кардинальное число 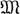≥ 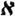₀ является калибром Д. б. (см. Калибр пространства). Отсюда вытекает существование недиадич. бикомпактов. Таковы, напр., все бикомпакты Александрова несчетной мощности (бикомпактификация одной точкой бесконечных дискретных пространств). В Д. б. всякое канонич. замкнутое множество и всякое замкнутое множество типа G₀ являются Д. б. Всякая неизолированная точка Д. б. есть ч-точка. Более того, если характер точки х ∈ Х равен 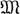≥ 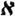₀, то в X содержится бикомпакт Александрова мощности 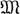, вершина к-рого совпадает с х. Вес бесконечного Д. б. равен верхней грани характеров его точек, а π-вес Д. б. равен его весу. Всякий экстремально несвязный Д. б. состоит из конечного множества точек. Существуют разнообразные критерии метризуемости Д. б. В частности, Д. б. X метризуем, если выполнено одно из следующих условий: X удовлетворяет первой аксиоме счетности; X является непрерывным образом упорядоченного бикомпакта; X наследственно нормален; X наследственно диадичен; X является пространством Фреше-Урысона; X наследственно сепарабелен; X является факторпространством метрич. пространства.

Лит.: [1] Engelking R., An Outline of General Topology, Amst., 1968; [2] Келли Дж. Л., Общая топология, пер. с англ., М., 1968; [3] Ефимов Б. А., «Тр. Моск. матем. о-ва», 1965, т. 14, с. 211-47.

А. В. Архангельский, Б. А. Ефимов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.