ДИАДА

ДИАДА - аффинор в гильбертовом пространстве х → (а, х)b,

где а, b - некоторые постоянные векторы, (⋅, ⋅) - скалярное произведение. Значение Д. состоит в том, что, напр., в n-мерном пространстве всякий аффинор А представляется в виде суммы не более чем n Д.:

Ax = 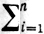(a_i, x)bⁱ

(в произвольном гильбертовом пространстве подобное разложение имеет место для частных классов линейных операторов, напр. для самосопряженных операторов, причем а_i и bⁱ образуют биортогоналъную систему). В 19 в. делались попытки положить понятие Д. в основу теории аффиноров - так называемое «диадное исчисление», в настоящее время термин Д. малоупотребителен.

Лит.: [1] Дубнов Я. С., Основы векторного исчисления, 4 изд., ч. 1,2, М.-Л., 1950-52; [2] Лагалли М., Векторное исчисление, пер. с нем., М.-Л., 1936; [3] Чепмен С, Каулинг Т., Математическая теория неоднородных газов, пер. с англ., М., 1960.

М. И. Войцеховский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.