ДИАГРАММА

ДИАГРАММА в категории С - отображение D ориентированного графа Г с множеством вершин I и с множеством дуг U в категорию С, при котором

D(I) ⊂ Ob(b), D(U) ⊂ Моr(b),

причем D(u) ∈ Hom(D(i), D (j)), если дуга u ∈ U имеет начало i и конец j. Иногда под диаграммой в С понимается образ отображения D, что позволяет использовать наглядное изображение диаграммы.

Пусть φ = (u₁, ... , u_n) - ориентированная цепь графа Г с началом i и концом j, т. е. непустая конечная последовательность дуг, в к-рой началом каждой дуги служит конец предыдущей; и пусть D(φ): D(i) → D(j) означает композицию морфизмов:

D(u_n) ○ ... ○ D(u₁).

Диаграмма D называется коммутативной, если D(φ) = D(φ') всякий раз, как φ и φ', являются ориентированными цепями с одним и тем же началом и концом.

Наиболее часто встречаемые виды Д. - это последовательности, треугольные диаграммы и квадратные диаграммы. Для определения последовательности за определяющий граф берется граф вида

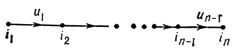
Соответствующая Д. изображается следующим образом:

здесь A_k = D(i_k) - объекты категории С, a f_k = D(u_k) - морфизмы этой категории.

Треугольная Д. в категории С соответствует графу

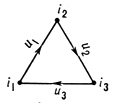
и изображается:

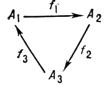
Коммутативность этой Д. означает, что f₃ = f₂ ○ f₁.

Квадратная Д. соответствует графу

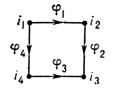
и изображается:

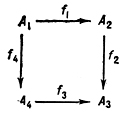
Коммутативность этой Д. означает, что f₂ ○ f₁ = f₃ ○ f₄.

Класс Д. с одним и тем же графом Г образует категорию. За морфизм диаграммы D в диаграмму D' принимается семейство морфизмов ν_i : D(i) → D'(i), где i пробегает множество вершин графа Г, что для любой дуги u с началом i и концом j выполняется условие D'(u) ○ ν_i = ν_j ○ D(u). В частности, можно говорить об изоморфных Д. Любую категорию можно представить как категорию диаграмм с нек-рым графом. Иногда граф Г наз. схемой диаграмм в С.

Лит.: [1] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961.

И. В. Долгачев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.