ДИАГОНАЛЬНОЕ ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ

ДИАГОНАЛЬНОЕ ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ f_α: X → Y_α, α ∈ 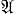, - отображение f: X → Y = π{Y_α, α ∈ 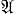}, определяемое равенством f(x) = {f_α(x)} ∈ Y. Д. п. о. f_α удовлетворяет для любого α соотношению f_α = π_αf, где π_α обозначает проектирование произведения Y на сомножитель Y_α. Диагональное произведение непрерывных отображений непрерывно. Семейство отображений f_α: X → Y_α наз. расчленяющим, если для любой точки х ∈ X и всякой ее окрестности Ох существует такой индекс α и такое открытое подмножество U_α ⊂ Y_α, что x ∈ f^-1_αU_α ⊂ Ox. Если {f_α: X → Y_α} - расчленяющее семейство отображений и f есть Д. п. о. f_α, то f является вложением пространства X в произведение πY_α, т. е. f : X → fX - гомеоморфизм. Д. п. о. было применено А. Н. Тихоновым для вложения вполне регулярного пространства веса τ в куб I^τ.

В. В. Федорчук

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.