ДЕФОРМАЦИЯ

ДЕФОРМАЦИЯ - 1) Д. аналитической структуры - семейство аналитич. пространств (или связанных с ними аналитич. объектов), зависящее от параметров. Теория Д. возникла из задачи классификации всевозможных попарно не изоморфных комплексных структур на данном вещественном дифференцируемом многообразии. Основная идея, восходящая к Б. Риману (В. Riemann), состояла здесь в том, чтобы ввести аналитич. структуру на множестве всех таких структур. Уточнением этой идеи являются следующие понятия. Аналитическим семейством комплексных многообразий, параметризованным комплексным пространством S, наз. любое гладкое (т. е. локально устроенное как проекция прямого произведения с гладким слоем) аналитич. отображение π : X → S. Если S связно, то все слои X_s, s ∈ S, отображения π диффеоморфны фиксированному слою Х_o, где o ∈ S, и могут рассматриваться как семейство комплексных структур на Х_o, аналитически зависящее от параметра s ∈ S. Если семейство X содержит в качестве слоев все комплексные многообразия, диффеоморфные Х_o, причем все слои попарно не изоморфны, то S наз. пространством модулей вещественного многообразия Х_o. Можно определить также пространство модулей для многообразий, принадлежащих определенному классу. Проблема построения пространства модулей (или проблема модулей) была решена вначале для компактных римановых поверхностей (см. Римановых поверхностей конформные классы). Результаты такого рода, хотя и неполные, получены и для компактных многообразий комплексной размерности 2 (см. Аналитическая поверхность).

Для многообразий больших размерностей исследование проблемы модулей встречает значительные трудности. В связи с этим К. Кодаира и Д. Спенсер [6], [7], [8] предприняли локальное изучение проблемы модулей, заложив тем самым основы теории Д. комплексных многообразий и аналитич. расслоений. Аналитической деформацией комплексного многообразия Х_o наз. аналитич. семейство π : X → S, причем S - комплексное пространство с отмеченной точкой о, слой над к-рой совпадает с Х_o. Деформация Х = X_o × S наз. тривиальной. Д. π̅ : X̅ → S многообразия Х_o наз. изоморфной Д. π : X → S, если существует аналитич. изоморфизм φ : Х̃ → Х, тождественный на Х_o и такой, что π ○ φ = π̅. Если π : X → S - аналитич. Д., то всякое аналитич. отображение f : S' → S, где о' - пространство с отмеченной точкой о' и f(о') = о, определяет при помощи замены базы Д. X ×_S S' → S' - обратный образ данной Д. при отображении f. Деформация π : X → S наз. локально полной (в точке о), если любая аналитич. Д. π': X' → S' многообразия Х_o изоморфна в нек-рой окрестности отмеченной точки ее обратному образу при нек-ром локальном аналитич. отображении f : S' → S. Если при этом df_o' - определено однозначно, то Д. наз. версальной в точке о, а если однозначно определен росток отображения f, - то универсальной. Важную роль в теории играет линейное отображение Т_o(S) → H¹(Х_o, Θ), где Θ = Θ_Xo - пучок ростков голоморфных векторных полей на Х_o, к-рое сопоставляется аналитич. Д. и наз. соответствующей инфинитезимальной деформацией.

Основная теорема локальной теории Д., доказанная М. Кураниси [9], утверждает, что для каждого компактного комплексного многообразия Х_o существует версальная в точке о Д., параметризованная (не обязательно гладким) аналитич. подпространством S в окрестности нуля пространства Н(Х_o, Θ). При этом S - слой в точке о нек-рого локального аналитич. отображения γ : H¹(Х_o, Θ) → H²(Х_o, Θ), имеющего вид γ(ξ) = [ξ, ξ] + ..., где [,] - операция в градуированной алгебре Ли Н^*(Х_o, Θ), индуцированная скобкой Ли в пучке Θ, а точки означают члены порядка ≥ 3. Если H¹(Х_o, Θ) = 0, то многообразие Х_o является жестким, т. е. любая его Д. локально тривиальна (теорема жесткости Фрёлихера-Нейенхёйса). Если Н²(Х, Θ) = 0, то S - окрестность нуля в H¹(Х_o, Θ). Касательное пространство T_o(S) всегда совпадает с H¹(X_o, Θ). Д. является полной в точке 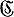тогда и только тогда, когда соответствующая инфинитезимальная Д. сюръективна, а версальность равносильна биективности инфинитезимальной Д. Если dim H⁰(X_s, Θ_Xs), s ∈ S, постоянна в окрестности нуля, то деформация Кураниси является универсальной.

Локальная теория Д. компактных комплексных многообразий обобщается на случай компактных комплексных пространств. При этом вместо гладкости отображения π: X → S и компактности слоя требуют, чтобы π было плоским и собственным отображением. Здесь также можно доказать существование версальной в точке о Д. (см. [3], [5], [11]).

Изучаются также Д. ростков аналитич. пространств (или, что равносильно, аналитич. алгебр). Справедлива теорема о существовании версальной Д. для изолированной особой точки комплексного пространства [4].

Наряду с теорией Д. комплексных пространств существуют теории Д. различных «аналитических объектов» - аналитич. расслоений, подпространств, отображений, классов когомологий, аналитич. пространств с дополнительной структурой (напр., с поляризацией) и др. Основные определения и проблематика этих теорий аналогичны описанным выше. Результаты, полученные для главных аналитич. расслоений, также аналогичны перечисленным выше. В частности, для любого главного аналитического расслоения Е с компактной базой X и комплексной группой Ли G в качестве структурной группы существует версальная в точке о Д. расслоения Е, параметризованная аналитич. подпространством в окрестности нуля пространства H¹(Х, 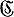_AdE), где 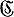_AdE - пучок ростков голоморфных сечений векторного расслоения над X, ассоциированного с Е при помощи присоединенного представления [1]. Если X - компактная риманова поверхность, а G - редуктивная алгебраич. группа, то можно построить пространство модулей для стабильных главных аналитич. расслоений. В теории Д. подпространств, напротив, получены весьма общие результаты глобального характера. А именно, если X - произвольное комплексное пространство ограниченной размерности, то построено [2] плоское аналитич. семейство компактных аналитич. подпространств в X (т. е. аналитич. подпространство Y ⊂ X × S, где S - комплексное пространство и проекция Y → S есть собственное плоское отображение), являющееся универсальной (в глобальном смысле) Д. для любого компактного аналитич. подпространства в X. В частности, S является пространством модулей для рассматриваемой задачи. Аналогичная проблема модулей решена в относительном случае, а также для компактных аналитич. циклов заданного комплексного пространства. Из решения проблемы модулей для компактных подпространств следует решение проблемы модулей и для аналитич. отображений заданного компактного комплексного пространства в другое заданное комплексное пространство.

Существуют попытки унификации упомянутых выше теорий Д. С каждой из этих теорий можно связать контравариантный функтор D из категории аналитич. пространств (или ростков аналитич. пространств) в категорию множеств. Напр., в теории локальных Д. комплексного пространства Х_o множество D (S) состоит из классов локально изоморфных Д. пространства Х_o, параметризованных ростком аналитич. пространства S. Если фиксировать S и элемент δ ∈ I)(S), то возникает морфизм функторов Моr(⋅, S) → D. Сюръективность этого морфизма (пара (S, δ) наз. в этом случае полной) соответствует свойству полноты Д. δ, а биективность - свойству ее универсальности. Проблема модулей связана, таким образом, с вопросом о представимости функтора D. В связи с этим было предпринято изучение ковариантных функторов из категории артиновых колец в категорию множеств, удовлетворяющих нек-рым естественным условиям [12]. Существование полной пары доказывается, однако, лишь в категории формальных алгебр, что соответствует существованию формальной полной Д. (см. Деформация алгебраического многообразия).

Обобщением теории Д. комплексных структур на многообразии является теория Д. псевдогрупповых структур, в к-рой рассматриваются семейства псевдогрупповых структур, гладко зависящие от параметра, принимающего значения в вещественном аналитич. пространстве. В частности, для псевдогрупповой структуры на компактном гладком многообразии, соответствующей эллиптич. транзитивной псевдогруппе преобразований, доказано существование версального ростка деформации [10].

Лит.: [1] Донин И. Ф., «Матем. сб.», 1974, т. 94, № 3, с. 430-43; [2] Dоuadу А., «Аnn. Inst. Fourier», 1966, t. 16, p. 1-95; [3] его же, «Аnn. sci. Ecole norm. sup.», 1974, т. 7, № 4, p. 569-602; [4] Grauert H., «Invent. math.», 1972, Bd 15, № 3, S. 171-98; [5] его же, там же, 1974, Bd 25, №2, S. 107-42; [6] Kodaira K., Spencer D. C., «Ann. Math.», 1958, v. 67, № 2, p. 328-401; [7] их жe, там же, 1958, v. 67, № 3, p. 403-66; [8] иx жe, там же, 1960, v. 71, № 1, p. 43-76; [9] Kuranishi M., в кн.: Proceedings of the Conference on Complex Analysis, Minneapolis. 1964, N. Y.-В., 1965, p. 142-54; [10] Moolgavkar S. H., «Trans. Amer. Math. Soc.», 1975, v. 212, № 485, p. 173-97; [11] Палaмодов В. П., «Успехи матем. наук», 1976, т. 31, № 3, с. 129-194; [12] Шлезингер М., «Математика», 1971, т. 15, № 4, с. 115-29.

А. Л. Онищик, Д. А. Пономарев.

2) Д. алгебраического многообразия - включение алгебраич. многообразия в семейство алгебраич. многообразий. Теория Д. алгебраич. многообразий и схем представляет собой алгебраич. аналог теории Д. аналитич. структур. Ее основными вопросами являются следующие:

Существование подъема. Дана схема Х₀ над полем k, схема S, точка s₀ ∈ S с полем вычетов k(s₀) = k. Существует ли плоская S-схема X, для к-рой слой X_S0 над точкой s₀ изоморфен Х₀? (S-схема X наз. деформацией, или подъемом, схемы Х₀ над S).

Проблема универсальности. Существует ли версальная (соответственно универсальная) Д. схемы X₀, т. е. такая Д. М над схемой Х₀, что для любой другой Д. X → S найдется (соответственно единственный) морфизм S → M, для которого X ≊ M ×_M S?

Каждая Д. X → S схемы Х₀ с помощью операции формального пополнения вдоль слоя X_S0 определяет формальную деформацию χ над пополнением локального кольца 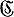_S,s0 схемы S в точке s₀, т. е. плоскую формальную схему над ̂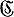_S,s0 с топологич. пространством Х₀. Формальные аналоги перечисленных выше вопросов формулируются следующим образом:

Существование формальной Д. Дано полное локальное кольцо Λ с полем вычетов k. Существует ли плоская формальная схема над Λ с топологическим пространством Х₀?

Существование формальной схемы модулей. Существует ли формальная версальная (соответственно универсальная) Д., т. е. плоская формальная схема р : χ → 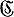над полным локальным кольцом 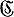с полем вычетов k такая, что для любой формальной Д. χ' → Spec Λ имеется (соответственно единственный) гомоморфизм колец 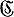→ Λ, для которого χ' ⊗ χ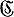Λ?

Универсальная формальная Д. гладкого многообразия представляет собой алгебраич. аналог локального пространства модулей в теории Д. аналитич. структур.

Если S = Spec R, где R - локальное артиново (соответственно полное) кольцо с полем вычетов k, то Д. Х₀ над S наз. инфинитезимальной (соответственно эффективной формальной). В случае, когда R - полное локальное кольцо характеристики нуль (напр., кольцо Витта векторов), эффективная формальная Д. Х₀ наз. подъемом Х₀ в характеристику нуль.

Если Х₀ - гладкая k-схема и H²(Х₀, Т_X0) = 0, где Т_X0 - касательный пучок на X₀, то для любого артинова (соответственно полного) локального кольца существует инфинитезимальная (соответственно формаль-

ная) Д. X₀. При этом, если Н¹(X₀, Т_X0) = 0, то такая Д. единственна с точностью до изоморфизма (см. [4]). Аналогичные утверждения для необязательно гладких схем даются в терминах кокасательного комплекса (см. [5], [6]). Вопрос о существовании эффективной формальной Д. изучается с помощью рассмотрения функтора D_X0 из категории C_k артиновых локальных колец с полем вычетов k в категорию множеств, к-рый сопоставляет каждому объекту R из C_k множество всех инфинитезимальных Д. Х₀ над R. Универсальная формальная Д. Х₀ существует в том и только в том случае, когда функтор является пропредставимым функтором. При этом пропредставляющий объект - полное локальное кольцо М_X0 с полем вычетов k - наз. формальной схемой модулей k-схемы Х₀. Формальная версальная Д. р : χ̃ → M̃_X0 существует, если Х₀ собственна над к или Х₀ есть аффинная схема конечного типа над k с изолированными особыми точками (см. [2], [6]). Версальная формальная Д. является универсальной, если для любого сюръективного гомоморфизма R' → R локальных артиновых колец и Д. X' → R' из D_X0(R') естественное отображение групп автоморфизмов

Aut_R' (X' | Х₀) → Aut_R(X'_R' ⊗ R | Х₀)

является сюръективным. Это условие выполняется, напр., если Х₀ - гладкая схема и Н⁰(Х₀, T_X0) = 0. При этом, если Н²(Х₀, Т_X0) = 0, то формальная схема модулей М_X0 является полным регулярным локальным кольцом, изоморфным кольцу k[[t₁, ..., t_m]] формальных степенных рядов от m переменных. Число m равно в этом случае dim_kH¹(X₀, Т_X0) и наз. числом локальных модулей схемы Х₀. В общем случае dim_kH¹(Х₀, Т_X0) равна размерности касательного пространства к М_X0 и M̃_X0, т. е. размерности dim_k m/m², где m - максимальный идеал соответствующего локального кольца, а

dim_kH¹(X₀, T_X0) - dim M_X0 ≤ dim_kH²(X₀, Т_X0).

Наличие нильпотентных элементов в формальной схеме модулей представляет довольно частое явление.

Если версальная (соответственно универсальная) формальная Д. χ → М_X0 алгебраизуема, т. е. существует плоская схема над М_X0, формальное пополнение которой вдоль замкнутого слоя изоморфно χ, то соответствующая алгебраизация наз. локальной версальной (соответственно универсальной) Д. k-схемы Х₀. Если Х₀ проективна и Н²(Х₀, Т_X0) = 0, то алгебраизация существует. Напр., для полной гладкой кривой рода g > 1 существует локальная универсальная Д. над кольцом k[[t₁, ..., t_3g-3]]. В общем случае, для каждой поляризации α многообразия Х₀ существует максимальная замкнутая подсхема в формальной схеме модулей М_X0,α ⊂ _X0 такая, что р^-1(М_X0,α) алгебраизуема. Коразмерность М_X0 в М_X0 не превышает dim_kH²(Х₀, _X0). Напр., если Х₀ - алгебраическая КЗ-поверхность, М_X0 регулярна размерности 20, а для любой поляризации а подсхема М_X0,α регулярна размерности 19.

Теорема Артина об аппроксимации применяется для алгебраизации формальной схемы модулей. Существует схема S конечного типа над k и точка s₀ ∈ S с полем вычетов k такая, что пополнение ̂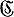_S,s0 М̂_X0, и существует Д. X₀ над S, индуцирующая версальную локальную Д. p̃: χ̂ → M̂_X0. Схема S определена однозначно с точностью до локального изоморфизма в этальной топологии [1]. Относительно Д. особых многообразий и особых точек см. Особая точка алгебраического многообразия. Относительно Д. групповых схем см. Групповая схема.

Лит.: [1] Артин М., «Математика», 1970, т. 14, № 4, с. 3-47; [2] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 12, М., 1974, с. 77-170; [3] Шлезингер М., «Математика», 1971, т. 15, № 4, с. 115-29; [4] Revêtements étales et groupe fondamental (SGA 1), В.- Hdlb.-N. Y., 1971; [5] Rim D. S., в кн.: Groupes de monodromie en géométric algébrique (SGA71), В.-Hdlb.-N. Y., 1972, p. 32-132; [6] Mumford D., в кн.: Zаriski O., Algebraic surfaces, 2 ed., В.-Hdlb.-N. Y., 1971, p. 118-28.

И. В. Долгачев.

3) Д. алгебры - семейство алгебр, зависящее от параметров. Всевозможные билинейные операции или алгебры 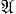в пространстве V над полем к образуют векторное пространство А(V). Два элемента этого пространства представляют изоморфные алгебры тогда и только тогда, когда они лежат на одной орбите линейной группы GL(V), естественным образом действующей в A(V). Теория Д. алгебр позволяет исследовать локальное строение фактормножества A(V)/GL(V), т. е. множества классов изоморфных алгебр в пространстве V, прямое описание к-рого связано с большими трудностями. Если выделен нек-рый класс алгебр К ⊆ А(V), то можно рассматривать Д. алгебр из класса K, не выводящие за пределы этого класса. В частности, рассматриваются Д. ассоциативных, ассоциативно-коммутативных алгебр и алгебр Ли, образующие классы K = Ass(F), K = Comm(F), K = Lie(V), соответственно, инвариантные относительно действия группы GL(V). Если dim V = n, то эти классы являются алгебраич. многообразиями в n³-мерном пространстве A(V).

Теория Д. алгебр в конечномерном пространстве V над полем k = ℝ и ℂ действительных или комплексных чисел во многом аналогична теории деформаций аналитич. структур. Каждая конечномерная алгебра 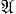над k = ℝ или ℂ обладает полной Д., параметризованной ростком аналитич. подпространства в нуле пространства H²(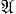, V) [если H³(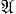, V) = 0, то это подпространство совпадает с Н²(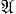, V)]. Из этого основного результата непосредственно следует теорема жесткости: если Н²(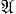, V) = 0, то алгебра 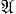является жесткой в K, т.е. орбита элемента 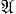относительно GL(V) открыта в K. Напр., жесткими в классе алгебр Ли являются полупростые алгебры Ли, а также их подалгебры Бореля. Утверждение, обратное к теореме жесткости, неверно. Аналогичные утверждения справедливы для конечномерных алгебр над произвольным алгебраически замкнутым полем k. Например, если

H²(G, V) = 0, то орбита алгебры 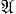в K̃ открыта по Зарискому.

Аналогично может быть развита теория Д. гомоморфизмов одной конечномерной алгебры в другую. На самом деле, описанные выше теории включаются в общую схему, использующую аппарат градуированных алгебр Ли. Сходные результаты получены также для Д. подалгебр.

Наряду с указанной выше теорией существует теория формальных Д. алгебр и их гомоморфизмов над произвольным полем k. Формальной Д. алгебры, заданной в векторном пространстве V над k, наз. алгебра на пространстве V ⊗ k((t)) над полем k((t)) формальных степенных рядов над k с операцией ○, к-рая полностью определяется условием

a ○ b = ab + 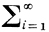φ_i(a, b)tⁱ, a, b ∈ V,

где φ_i ∈ A(V). Требуя, чтобы Д. принадлежала данному классу алгебр, можно говорить о формальных Д. ассоциативных, ассоциативно-коммутативных, лиевых и других алгебр.

Две формальные Д. алгебры 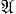с умножениями × и ○ соответственно наз. эквивалентными, если существует линейный автоморфизм Ф пространства V ⊗ k((t)) со свойством

Ф(а) = a + 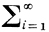tⁱφ_i(a), a ∈ V,

где φ_i : V → V - линейное отображение такое, что а ○ b = Ф^-1(Ф(a) × Ф(b)).

Д., эквивалентная алгебре 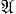с исходным умножением, наз. тривиальной. Алгебра, не имеющая нетривиальных формальных Д. в данном классе алгебр, наз. формально жесткой в этом классе. Напр., свободная алгебра в классе всех алгебр будет формально жесткой. В классах Ass(F), Comm(F), Lie(V) достаточным условием формальной жесткости алгебры 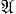является равенство H²(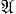, V) = 0. В классе Ass(F) это условие является также и необходимым [3].

В случаях k = ℝ или ℂ формальные Д. алгебр служат аппаратом для изучения аналитич. Д.

Важной областью приложений и источником примеров Д. алгебр является теоретич. физика, где, в частности, возник следующий класс Д. алгебр (см. [4], [5]). Стягиванием конечномерной алгебры 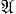над k = ℝ или ℂ наз. непрерывная кривая 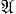_t, 0 ≤ t ≤ 1, в пространстве А(V) такая, что 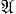_t = 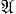при 0 ≤ t < 1. Алгебра 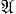₁, полученная из 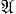в результате стягивания, наз. предельной и может не быть изоморфной алгебре 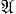. Напр., любую алгебру можно стянуть в алгебру с нулевым умножением; любую полупростую алгебру Ли можно стянуть в неабелеву неполупростую.

Лит.: [1] Niienhuis A., Richardson R. W. Jr., «Bull. Amer. Math. Soc.», 1966, v. 72, № 1, p. 1-29, 1967, v. 73, № 1, p. 175-79; [2] Gerstenhaber M., «Ann. Math.», 1964, v. 79, p. 59-103; [3] Knudson D., «Trans. Amer. Math. Soc.», 1969, v. 140, p. 55-70; [4] Inönu E., Wigner E. P., «Рrос. Nat. Acad. Sci. USA», 1953, v. 39, № 6, p. 510-24; [5] Hermann R., Lie groups for physicists, N. Y.- Amstard., 1966.

А. А. Бояркин, А. В. Михалев, А. Л.Онищик.

4) Д. подмножества А пространства X - гомотопия:

D: A × I → X,

для к-рой D(а, 0) = а при а ∈ А. Если, более того, множество D(A × I) принадлежит нек-рому подпространству X' пространства X, то D наз. Д. А в X', а А наз. деформируемым в X' в пространстве X. Пространство X наз. деформируемым в подпространство X', если оно деформируемо по себе в X'. В частности, X стягиваемо тогда и только тогда, когда оно деформируемо в одну из своих точек. Пространство X деформируемо в подпространство X' тогда и только тогда, когда для вложения i: X' → Х существует правое чески обратное отображение r : X → Х', т. е. i ○ r ~ 1. Понятие Д. всего пространства по себе на подпространство родственно понятию слабой ретракции.

М. И. Войцеховский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.