ДЕФЕКТНОЕ ЗНАЧЕНИЕ

ДЕФЕКТНОЕ ЗНАЧЕНИЕ мероморфной функции f - комплексное число а (конечное или бесконечное), дефект к-рого (см. ниже) δ(а, f) положителен. Функция f определена в круге |z| < R ≤ ∞ комплексной плоскости ℂ. Дефект значения а:

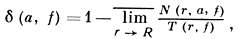
где Т(r, f) - характеристическая функция Неванлинны, отражающая рост f при r → R, и

N(r, а, f) = 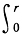[n(t, а) - n(0, a)] d ln t + n(0, a) ln r

- считающая функция; здесь n(t, а) - число решений уравнения f(z) = a в круге |z| ≤ t (с учетом кратностей). Если Т(r) → ∞ при r → R, то 0 ≤ δ(а, f) ≤ 1 для всех a ∈ ℂ ∪ {∞}. Если f(z) ≢ a ни для какого z, то δ(а, f) = 1 и а есть Д. з.; это равенство возможно и в более общем случае (напр., f(z) = ze^z, R = ∞ и a = 0). Если

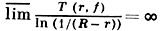
(или f ≢ const мероморфна во всей плоскости), то ∑_a(a, f) ≤ 2 (соотношение дефектов), и число Д. з. для такой f не более чем счетно. В остальном множество Д. з. может быть произвольным; напр., для любых последовательностей {a_ν} ⊂ ℂ и {δ_ν} ⊂ ℝ⁺, ∑_νδ_ν ≤ 1, найдется целая функция f такая, что

δ(a_ν, f) = δ_ν для всех ν и других Д. з. у f нет. Ограничения на рост f влекут за собой ограничения на Д. з. и их дефекты. Напр., мероморфная функция нулевого порядка или целая функция порядка < 1/2 не могут иметь более одного Д. з. Число

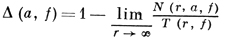
(f мероморфна в ℂ) наз. дефектом в смысле Валирона. Множество чисел а, для к-рых Δ(а, f) > 0, может иметь мощность континуума, но всегда имеет нулевую логарифмич. емкость.

См. также исключительное значение, Распределения значений теория.

Лит.: [1] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.-Л., 1941; [2] Xейман У., Мероморфные функции, пер. с англ., М., 1966; [3] Гольдберг А. А., Островский И. В., Распределение значений мероморфных функций, М., 1970.

Е. М. Чирка

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.