ДЕТЕРМИНАНТНОЕ МНОГООБРАЗИЕ

ДЕТЕРМИНАНТНОЕ МНОГООБРАЗИЕ - множество матриц D_t(d, n) порядка d × n и ранга меньше t, снабженное структурой алгебраич. многообразия. Пусть J_t(d, n) - идеал кольца многочленов

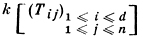
с коэффициентами в поле k, порожденный минорами порядка t матрицы порядка d × n, составленной из переменных T_ij (детерминантный идеал). Множество нулей идеала J_t(d, n) в аффинном пространстве A^dn = Spec(k[(T_ij)]) наз. детерминантным многообразием и обозначается D_t(d, n). Для любой коммутативной k-алгебры k' множество k'-точек Д. м. D_t(d, n) естественным образом отождествляется с множеством матриц порядка d × n и ранга < t с коэффициентами в k'.

Частные случаи Д. м.: D_d(d, d) есть гиперповерхность в A^d₂, задаваемая обращением в нуль определителя квадратной матрицы порядка d, составленной из независимых переменных (детерминатная гиперповерхность); D₂(d, n) есть аффинный конус для образа вложения Сегре

P^d-1 × P^n-1 → P^dn-1

произведения проективных пространств [2].

Д. м. обладают следующими свойствами: D_t(d, n) неприводимо, приведено (т. е. идеал J_t(d, n) прост), является многообразием Коэна-Маколея (см. Коэна-Маколея кольцо), нормально, и размерность D_t(d, n) равна (t - 1)(n + d - 1) (см. [1], [2]). При t = 1 или d = n (и только в этих случаях) D_t(d, n) является схемой Горенштейна (см. Горенштейна кольцо) [5]. Д. м. тесно связаны с подмногообразиями Шуберта грассманова многообразия (см. Шуберта многообразие).

Лит.: [1] Hochster М., Еagоn J., «Аmеr. J. Math.», 1971, v. 93, № 4, р. 1020-58; [2] Kleiman S., Landolfi J., «Compositio math.», 1971, v. 23, p. 407-34; [3] Laksov D., «Соmp. math.», 1975, v. 34), p. 273-92; [4] Musili C. «J. Indian Math. Soc.», 1974, v. 38, p. 131-45; [5] Svanes Т., «Advances Math.», 1974, v. 14, p. 369-453.

И. В. Долгачев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.