ДЕСЯТИЧНАЯ ДРОБЬ

ДЕСЯТИЧНАЯ ДРОБЬ - дробь (арифметическая), знаменателем к-рой является целая степень числа 10. Для Д. д. принята запись

a_ka_k-1 ... a₁a₀, b₁b₂ ... b_l (1)

где 0 ≤ а_i, b_j < 10 - целые числа, причем, если k ≠ 0, то и a_k ≠ 0.

Под (1) понимается число, равное

a_k10^k + a_k-110^k-1 + ... + a₁10 + a₀ + b₁/10 + b₂/10² + ... + b_l/10^l.

Напр.,

3/10 = 0,3; 3524/100 = 35,24; 15/1000 = 0,015.

Цифры, стоящие после запятой, наз. десятичными знаками. Если Д. д. не содержит целой части, т. е. меньше единицы по абсолютной величине, то перед запятой ставится нуль.

Бесконечной десятичной дробью наз. бесконечный ряд чисел вида:

a₀, b₁b₂...,(2)

где а₀ - целое число, а каждое из чисел b_j (j = 1, 2, ...) принимает одно из значений 0, 1, 2, ..., 9. Любое действительное число α является суммой некоторого такого ряда, т. е.

α = a₀ + 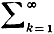b_k/10^k.

Частные суммы ряда (2) - конечные Д. д. а₀, b₁ ... b_n, являются приближенными значениями числа α с недостатком, а числа

a₀, b₁...b_n + 1/10ⁿ,(2)

- приближенными значениями с избытком. Если существуют такие целые числа n и m, что для всех i > n имеют место равенства

b_i = b_i+m,

то бесконечная Д. д. наз. периодической. Всякую конечную Д. д. можно рассматривать как бесконечную периодическую с b_i = 0 для i #62; n. Если α - рациональное число, то соответствующая ему дробь (2) будет периодической. Для иррационального числа α дробь (2) периодической быть не может.

С. А. Степанов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.