ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ

ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ - раздел теории множеств, изучающий внутреннее строение множеств в зависимости от тех операций, при помощи к-рых эти множества могут быть построены из множеств сравнительно простой природы (напр., замкнутых или открытых подмножеств данного евклидова, метрич. или топологич. пространства). К указанным операциям относятся объединение, пересечение, взятие дополнения, проектирование и т. д. Д. т. м. зародилась в начале 20 в. в трудах Э. Бореля (Е. Borel), Р. Бэра (R. Baire) и А. Лебега (Н. Lebesgue) в связи с проблемой измеримости множеств. Множества, измеримые по Борелю, получили название борелевских множеств, или B-множеств. С другой стороны, Р. Бэр дал классификацию функций, названных впоследствии бэровскими функциями, и доказал ряд теорем об этих функциях (см. Бэра классы, Бэра теорема). А. Лебег доказал, что B-множества тождественны Лебега множествам бэровских функций, дал первую классификацию B-множеств и доказал непустоту каждого ее класса.

Изучение B-множеств стало важной задачей Д. т. м., причем в первую очередь надлежало выяснить вопрос о мощности B-множеств. После введения Лебега меры оказалось, что класс измеримых множеств значительно шире класса B-множеств, и возник вопрос об отыскании средств установления измеримости того или иного множества. Решение этого вопроса в каждом конкретном случае связано, как правило, с выяснением того процесса, при помощи к-рого это множество может быть построено, т. е. его дескриптивной структуры. Так определился еще один важный круг задач Д. т. м.- отыскание возможно более широкого класса (сохраняющих измеримость) операций над множествами и исследование свойств результатов этих операций. Решение этих вопросов, возникших в работах французских математиков, было дано преимущественно русскими математиками - Н. Н. Лузиным и его школой.

Один из наиболее важных вопросов - вопрос о мощности Б-множеств - был решен П. С. Александровым [1] в 1916, построившим для этого А-операцию. Им было показано, что посредством A-операции, отправляясь от интервалов, можно построить любое В-множество и что всякое несчетное множество, полученное путем А-операции (и называемое A-множеством), содержит совершенное множество и, значит, имеет мощность континуума. Этот результат был независимо получен Ф. Хаусдорфом (F. Hausdorff). М. Я. Суслин [2] показал, что существует A-множество, не являющееся борелевским. Он же ввел и название A-множества, равно как и A-операции (в честь П. С. Александрова). А-множества наз. также суслинскими множествами или, реже, аналитическими множествами. Для того чтобы А-множество было B-множеством, необходимо и достаточно, чтобы: 1) дополнение к нему снова было А -множеством (Суслина критерий); 2) оно являлось результатом A-операции с непересекающимися слагаемыми (Лузина критерий). Все A-множества измеримы и обладают Бэра свойством. Были найдены следующие новые способы получения A-множеств, эквивалентные A-операции: A-множества суть проекции B-множеств (и даже G_δ); A-множества суть непрерывные образы пространства I иррациональных чисел; и, значит, A-множества суть непрерывные образы B-множеств [3]. В то же время, непрерывный взаимно однозначный (и даже счетнократный [4]) образ B-множества есть В-множество и всякое несчетное B-множество есть объединение не более чем счетного множества и непрерывного взаимно однозначного образа пространства I (см. [3]). Наконец, Н. Н. Лузиным был найден еще один важный способ задания A-множеств при помощи введенной им операции решета (см. Лузина решето). Трансфинитные индексы решета и конституанты стали мощным орудием исследования свойств A-множеств и их дополнений - СА-множеств.

При исследовании проблемы о мощности СА-множеств Н. Н. Лузин вводит проективные множества. Каждый класс α проективных множеств содержит множества, не принадлежащие классам < α (см. [3], [5]). Важным инструментом при доказательстве этой и других теорем о непустоте тех или иных классов множеств является понятие универсального множества (см. [3], [6], [5]). Изучение проективных множеств даже второго класса наталкивается на непреодолимые трудности. Так, не решен полностью вопрос об измеримости множеств (В₂), их мощности и о наличии у них свойства Бэра. Важные результаты в этом направлении получены П. С. Новиковым [4]: существует несчетное СА-множество, относительно к-рого непротиворечиво предположение, что оно не содержит совершенного подмножества; существует множество (В₂), относительно к-рого непротиворечиво утверждение, что оно неизмеримо.

Введение П. С. Александровым [7] Г-операции, дополнительной к A-операции, явилось первым шагом в направлении построенной А. Н. Колмогоровым [8] и Ф. Хаусдорфом [9] общей теории теоретико-множественных операций; однако основной класс операций составляют положительные теоретико-множественные операции, или δs-операции. Для каждой δs-операции Ф была определена дополнительная δs-операция Ф^c и дана формула

Ф^с({Е_n}) = С[Ф({СЕ_n})],

к-рая может рассматриваться как определение Ф^c. Было введено также понятие нормальной δs-операции (для любого семейства М множеств Ф(Ф(М))=Ф(М), см. [8]). A-операция и Г-операция являются взаимно дополнительными нормальными δs-операциями. То же самое справедливо относительно операций счетного объединения и счетного пересечения. Одной из ключевых теорем общей теории операций над множествами, лежащими в топологич. пространствах, является теорема Колмогорова о дополнениях: если пространство содержит дисконтинуум, М - система всех замкнутых подмножеств этого пространства и Ф - произвольная теоретико-множественная операция, то дополнение хотя бы одного множества семейства Ф(М) ему не принадлежит (см. [8], [5], [9]). Применение к данному семейству М множеств попеременно δs-операции Ф и Ф^c позволяет построить возрастающую трансфинитную последовательность классов М₀ = М, М₁, ..., М_α, α < ω₁ относительно к-рой верна теорема Колмогорова о непустоте классов: если Ф есть нормальная δs-операция более мощная, чем операции счетного объединения (или счетного пересечения), а М есть семейство всех замкнутых подмножеств метрич. пространства, содержащего дисконтинуум, то все классы М_α, α < ω₁ порождаемые операцией Ф из семейства М, попарно различны. При этом δs-операция Ф считается более мощной, чем δs-операция ψ, если Ф(М) ⊇ δ(М) для любого семейства М множеств (см. [8], [5]). 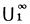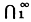Если Ф = (или ), то классы М_α, α < ω₁, порожденные операцией Ф из семейства М, представляют собой классы B-множеств, порожденных семейством М (классификация Хаусдорфа). Аналогичным образом A-операция порождает из семейства М борелевских множеств классы М_α, α < ω₁, С-множеств (Лузина множеств). Каждое С-множество измеримо и обладает свойством Бэра. Все С-множества входят в класс (В₂), но не исчерпывают его.

Исключительно важную роль в Д. т. м. играет введенное Н. Н. Лузиным понятие отделимости [4]. Первый принцип отделимости: всякие два непересекающиеся A-множества отделимы (В). Второй принцип отделимости: если Е и Р - два A-множества (или СА-множества), то множества Е\Р и Р\Е отделимы (СА). Существуют два СА-множества, неотделимые (В). Проблема отделимости проективных множеств второго класса была решена П. С. Новиковым [4]; при этом принципы отделимости оказались обращенными: они получаются из соответствующих теорем для проективных множеств первого класса заменой (A) на (СА₂), (СА) на (A₂) и (В) на (В₂). Проблема отделимости в классе С-множеств была также решена П. С. Новиковым [4] (см. также [3]). Им же введено обобщение понятия отделимости множеств - понятие одновременной или кратной отделимости множеств, равно как и основной инструмент при доказательстве теорем кратной отделимости - принцип сравнения индексов [4].

Важная глава в развитии Д. т. м. связана с решением проблемы униформизации. Множество Р униформизует множество Е ⊂ Х × Y, если P ⊂ E и если P имеет ту же, что и Е, проекцию на X и проектируется на X взаимно однозначно. Всякое B-множество униформизуется СА -множеством. Процесс эффективного выбора точки [4] в непустом СА-множестве позволил получить более сильный результат: всякое СА -множество униформизуется СА-множеством. Всякое A-множество униформизуется множеством типа A_ρσδ [3] (см. также [10]). Существует A-множество в евклидовой плоскости, не униформизуемое ни A-множеством, ни СА-множеством (см., напр., [11], с. 57). В вопросе о том, в каких случаях B-множество может быть униформизовано В-множеством, наиболее общий результат имеет вид: всякое плоское B-множество, пересекающееся с прямыми х #&8801; const по множествам типа F_σ, униформизуется B-множеством. Проблема униформизации возникла при решении проблемы о неявных B-функциях (см. [3]). При этом возникли и другие задачи: о природе проекций B-множеств, о расщеплении множеств, о накрытии множеств, о природе множества всех тех точек проекции данного B-множества Е, прообразы к-рых (в пересечении с Е) обладают нек-рым фиксированным свойством. Представление о второй и третьей задачах дают следующие теоремы [3]: B-множество, имеющее счетно-кратную проекцию, является объединением счетного числа униформных B-множеств, причем, каковы бы ни были два таких множества, одно из них лежит под другим (теорема о расщеплении В-множества); всякое A-множество, имеющее счетнократную проекцию, содержится в нек-ром B-множестве, обладающем этим свойством (теорема о накрытии A-множества).

Помимо классификаций B-множеств, принадлежащих А. Лебегу и Ф. Хаусдорфу, существует классификация Лузина-Валле Пуссена. В этой классификации в качестве инструмента для исследования строения множеств данного класса К_α, α < ω₁, выбраны множества, представимые в виде пересечения и не представимые в виде объединения счетного числа множеств классов < α; эти множества наз. элементами класса α. Всякое множество класса K_α есть объединение счетного числа попарно непересекающихся элементов классов ≤ α. Каждый

класс K_α разбивается на подклассы K^β_α, β < ω₁ причем в каждом классе существуют подклассы со сколь угодно большими номерами β < ω₁. Поскольку каждое множество класса α строится из элементов, то возник вопрос об исследовании строения самих элементов, в частности о существовании в каждом классе K_α такого основного топологич. типа элементов, названных каноническими, чтобы каждый элемент класса α мог быть представлен в виде объединения счетного числа

канонич. элементов классов ≤ α (все рассматривается в пространстве I иррациональных чисел). В первом классе имеются канонич. элементы двух типов - одноточечное множество и топологич. образ канторова совершенного множества. Во втором классе [12] каждый элемент есть объединение канонич. элемента класса 2, каковым является множество, гомеоморфное пространству I, и множества класса ≤ 1. Были найдены и канонич. элементы третьего класса: ими оказались элементы третьего класса, построенные Р. Бэром, к-рые являются каноническими (см. [3]). Проблема существования канонич. элементов высших классов, оказавшаяся исключительно грудной, была решена Л. В. Келдыш [13], установившей существование канонич. элементов в каждом классе α₁ < ω₁ и выяснившей их строение. Каждый элемент класса α > 2 является объединением одного канонич. элемента класса α и не более чем счетного числа множеств классов < v. Еще одна трудная задача из этого круга связана с построением арифметич. примеров B-множеств низших классов. Такой пример для класса 3 построен Р. Бэром (см. [3]). Арифметич. примеры элементов всех конечных классов даны Л. В. Келдыш [13] (см. также [3]), указавшей на принципиальную возможность построения таких примеров для классов α ≥ ω₁.

Важную роль в Д. т. м. играет Лаврентьева теорема о продолжении гомеоморфизма (см. [9]): пусть X и Y полные метрич. пространства, A ⊂ X, B ⊂ Y и f: А 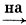В есть гомеоморфизм; тогда существует продолжение отображения f до гомеоморфизма двух C_δ -множеств, лежащих в этих пространствах. Из этой теоремы легко следует теорема о топологической инвариантности (см. [9]): пусть 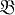- система замкнутых множеств и Ф - такая δ_s-операция, что пересечение Ф(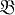)-множества (т. е. множества семейства Ф(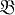) с G_δ-множеством есть снова Ф(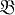)-множество; тогда каждое Ф(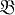) -множество, лежащее в полном метрич. пространстве, является Ф(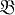)-множеством в любом метрич. пространстве, в к-ром оно топологически содержится. Система 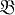в этой теореме может быть заменена системой 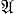открытых множеств. Таким образом, Ф(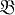)-множества, где Ф удовлетворяет указанному выше условию, лежащие в полных метрич. пространствах, являются абсолютными Ф(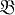)-множествами, и то же самое верно для Ф(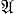)-множеств (при этом имеется в виду абсолютность в классе метрич. пространств). Для ряда частных случаев, напр. СA-множеств [7| (Ф есть Г-операция), этот результат был установлен без применения теоремы Лаврентьева. Всякое полное метрич. пространство есть абсолютное G_δ. Всякое (метризуемое) абсолютное G_δ гомеоморфно нек-рому полному метрич. пространству (теорема Александрова-Хаусдорфа, см. [9]).

Справедлива следующая теорема Александрова-Урысона [12] о топологич. характеристике пространства иррациональных чисел: каждое нульмерное метрич. пространство X со счетной базой, не имеющее ни одной точки локальной компактности и являющееся абсолютным G_δ, гомеоморфно пространству I. А так как I есть абсолютное G_δ и обладает всеми остальными свойствами пространства X, то перечисленные в теореме свойства пространства X полностью характеризуют пространство I с топологич. точки зрения. Эта характеризация позволила доказать следующий результат [14]: каждое метрич. пространство, являющееся непрерывным образом пространства I (и, значит, абсолютным A-множеством), есть также факторный образ пространства I. К этому кругу результатов принадлежат также следующие: непустое сепарабельное метрич. пространство есть непрерывный открытый образ пространства I тогда и только тогда, когда оно есть абсолютное Gδ (см. [15]); здесь «открытый» можно заменить на «замкнутый». Обобщением непрерывного отображения является понятие B-измеримого отображения, или B-функции, в частности, B-измеримого отображения класса α; обобщениями гомеоморфизма являются понятия обобщенного гомеоморфизма класса (α, β) и B-изоморфизма. Об этих отображениях см. [6].

При формулировке результатов, как правило, не указывался тот класс пространств, для к-рого они справедливы. Это объясняется тем, что большинство классич. результатов было получено для подмножеств пространства I, но почти все они (исключения всегда оговаривались) справедливы при замене I любым сепарабельным абсолютным G_δ (в частности, полным метрич. пространством со счетной базой). Дальнейшее развитие Д. т. м. проходило по линии обобщения классич. результатов для случая: 1) полных метрич. пространств (не обязательно сепарабельных); 2) совершенно нормальных топологич. пространств, в частности, бикомпактов; 3) общих топологич. пространств. Даже в первом случае обобщение классич. теории связано с серьезными трудностями, а часто и вовсе не имеет места. Обобщение теории B-множеств и A-множеств для этого случая рассмотрено А. Стоуном [16].

Класс совершенно нормальных пространств есть класс, за пределами к-рого уже не имеет места тот немаловажный факт, что система B-множеств (соответственно А-множеств), порожденных замкнутыми множествами данного пространства, совпадает с системой B-множеств (соответственно А-множеств), порожденных открытыми множествами этого пространства. Справедлива важная теорема о непустоте классов [11]: во всяком несчетном совершенно нормальном бикомпакте для каждого класса α < ω₁ существует B-множество класса α, не являющееся B-множеством класса < α.

Проблема униформизации стала частным случаем общей проблемы о сечении многозначного отображения (см. Сечение отображения).

Современная разработка Д. т. м. в общих топологич. пространствах (третий случай) имеет связь с потребностями других областей математики (напр., с теорией потенциала). Подробнее см. [17] (имеется обширная библиография).

Идеи и методы Д. т. м. оказали большое влияние на развитие целого ряда областей математики: анализа, теории функций, топологии, математической логики и др.

Лит.: [1] Александров П. С, «С. r. Acad. sci.», 1916, t. 162, p. 323-25; [2] Суслин М. Я., там же, 1917, t. 164, р. 88-90; [3] Лузин Н.Н., Собр. соч., т. 2, М., 1958; [4] Ляпунов А. А., «Тр. матем. ин-та АН СССР», 1973, т. 133, с. 11-22; [5] Очан Ю. С., «Успехи матем. наук», 1955, т. 10, в. 3, с. 71-128; [6] Куратовский К., Топология, т. 1, М., 1966; [7] Александров П. С., «Fundam. math», 1924, t. 5, p. 160-65; [8] Колмогоров A. H., «Матем. сб.», 1928, т. 35, № 3-4, с. 415-22; [9] Хаусдорф Ф., Теория множеств, пер. с нем., М.-Л., 1937; [10] Арсенин В. Я., Ляпунов А. А., «Успехи матем. наук», 1950, т. 5, в. 5, с. 45-108; [11] Пономарев В. И., «Докл. АН СССР», 1966, т. 170, № 3, с.520-23;[12] Александров П. С., Урысон П. С, «Math. Ann.», 1927, Bd 98, S. 89-106 (рус. пер. в кн.: Урысон П. С., Труды по топологии и другим областям математики, т. 2, М.-Л., 1951, с. 973-92); [13] Келдыш Л. В., «Тр. матем. ин-та АН СССР», 1945, т. 17, с. 1-76; [14] Michael Е., Stоnе А. Н., «Pacif. J. Math.», 1969, v. 28, № 3, p. 629-33; [15] Архангельский А. В., «Тр. Моск. матем. об-ва», 1966, т. 15, с. 181-223; [16] Stone A. Н., «General Topology and its Application», 1972, v. 2, p. 249-70; [17] Frolik Z., «Czechoslovak Mathematical Journal», 1970, v. 20, p. 406-67.

А. Г. Ельцин, В. И. Пономарев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.