ДЕЛИТЕЛЕЙ ПРОБЛЕМЫ

ДЕЛИТЕЛЕЙ ПРОБЛЕМЫ - проблемы теории чисел, касающиеся асимптотич. поведения сумматорных функций

D(x) = ∑_n≤x τ(n), D_k(x) = ∑_n≤x τ_k(n),

(где τ(n) - число делителей n, а τ_k(n), k ≥ 2, - число представлений n в виде произведения k натуральных чисел), а также модификаций этих функций.

Проблема делителей Дирихле - проблема наилучшей оценки остаточного члена Δ(х) в асимптотич. формуле

∑_n≤x τ(n) = х ln х + (2С - 1)х + Δх, где С - Эйлера постоянная. Асимптотика суммы

∑_n≤x τ(n) = D(x)

впервые рассмотрена П. Дирихле (P. Dirichlet) в 1849. Он исходил из того, что данная сумма равна числу точек (u, v) с целыми положительными координатами под гиперболой uv = x, и доказал, что

D(х) = х ln х + (2С - 1)х + O(√х).

Эта формула наз. формулой Дирихле числа делителей.

Д. п. явилась одной из тех моделей, на к-рых развивались методы оценок числа целых точек в разного рода расширяющихся областях. Пусть θ - нижняя грань чисел α в соотношении Δ(х) ≪ х^α. Согласно П. Дирихле, 0 ≤ 1/2. Г. Ф. Вороной доказал, что θ ≤ 1/3. Далее последовательно были получены оценки

θ ≤ 33/100, θ ≤ 27/82, θ ≤ 15/46, θ ≤ 13/40.

Истинный порядок величины Δ(х) (к 1978) неизвестен. Существует гипотеза, что

Δ(x) ≪ x^1/4 ln²х.

С другой стороны, X. Харди (Н. Hardy) доказал, что θ ≥ 1/4, или, точнее,

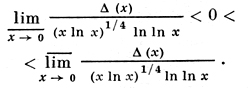
Кроме того, известна формула

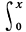 Δ²(y)dy = Ax^3/2 + O(x ln⁵ x)

(А - постоянная), показывающая справедливость «в среднем» гипотезы о порядке Δ(х).

Обобщенная проблема делителей - проблема наилучшего асимптотич. выражения при х → ∞ суммы

в частности, при k = 2

τ₂(n) = τ(n), D₂(x) = D(x).

Обобщенная Д. п. тесно связана с поведением дзета-функции Римана ζ(s) в критич. полосе значений s. Именно, для нецелого х > 0, с > 1 имеет место формула

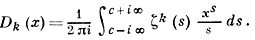
Здесь подинтегральная функция имеет в точке s = 1 полюс порядка k с вычетом вида хР_k(ln x), где Р_k - многочлен степени k - 1. Пусть

D_k(x) = xP_k(ln х) + Δ_k(х)

и пусть γ_k < γ < 1 где γ_k - нижняя грань чисел σ, для к-рых

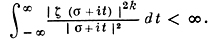
Тогда справедливы формула

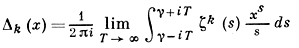
и обратная формула Меллина:

ζ^k(s)/s = 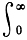Δ_k(x) x^-s-1 dx, s = &$963; + it,

где интеграл существует в смысле среднего квадратичного для γ_k < σ < 1.

Оценки остаточного члена Δ_k(х) в формуле D_k(х) еще далеки (к 1978) от ожидаемых. Пусть α_k - наименьшее из чисел α, для к-рых

Δ_k(х) ≪ x^α+ε

при любом ε > 0. Известны оценки:

α_k ≤ (k - 1)/(k + 1), α_k ≤ (k - 1) / (k + 2) для k ≥ 4.

Имеются уточнения этих оценок для частных значении k:

α₃ ≤ 37/75, α₇ ≤ 71/107, α₈ ≤ 41/59, α₉ ≤ 26/35, α₁₁ ≤ 19/25.

Последний результат оценки сверху α_k получен в [3] на основе развития идей Виноградова метода: доказано существование такой абсолютной постоянной с > 0, что

α_k ≤ 1 - c/k^2/3, k = 2, 3, ...

Эта оценка есть следствие оценки ζ(s) в критич. полосе: для 1/2 ≤ σ ≤ 1, |t| ≥ 2 существует такая постоянная a > 1, что

ζ(σ + it) ≪ |t|^a(1-σ)3/2 ln |t|.

С другой стороны, X. Харди (G. Hardy) доказал, что α_k ≥ (k - 1)/2k.

Относительно величины Δ_k(x) существует гипотеза:

α_k = (k - 1)/2k.

при всех k ≥ 2. Однако для ее обоснования недостаточно даже решения Линделёфа гипотезы:

ζ(σ + it) ≪ |t|^ε

при любых ε > 0, σ > 1/2.

Дальнейшее обобщение Д. п. [4]: равномерно относительно целых k ≥ 2, m ≥ 1 при x ≥ 1

1/x ∑_n≤x τ^m_k(n) < A^(m)_k (ln x + k^m - 1)^km-1

где

A^(m)_k = k^m / (k!)^{(km - 1)/(k - 1)}.

Проблема делителей в арифметических прогрессиях -проблема равномерных относительно х, d, 0 ≤ l ≤ d, (l, d) = 1, оценок сумм

∑_{n≤x,n≡l(mod d)} τ^m_k(n) = D^(m)_k(x; d, l).

Эти суммы изучались на основе аналитич. методов теории L-функций и важны для многих проблем теории чисел (см. [7]). В простейшем случае (m = 1) для них получены асимптотич. выражения:

при k = 2 для d ≤ x^2/3 (см. [5]), при k = 4 для d ≤ x^1/2 (см. [6]), при k ≥ 4 для d ≤ x^2/k ln^c х [см. [8]).

При любом m ≥ и k = 2 найден (см. [9]) истинный порядок роста (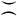) для d ≤ x^1-α, 0 < α < 1/2:

D^(m)₂(x; d, l) 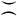x/d [ln x/d ∏_p|d (1 - 1/p)^2m-1].

В общем случае доказано [10J, что

∑_d≤x^1/2-ε max_l |D^(m)_k|(x; d, l) - A^(m)_k(x; d)| < x (ln x)^-M,

где A^(m)_k(х; d) - ожидаемый главный член роста, М - положительная сколь угодно большая постоянная, ε > 0 - любое число.

Последнее неравенство, в частности, показывает,

что суммы D^(m)_k(х; d, l) при любых целых k ≥ 2, m ≥ 1 «в среднем» имеют один и тот же главный член роста для всех примитивных арифметич. прогрессий разности

d ≤ x^1/2-ε.

Лит.: [1] Титчмарш Е. К., Теория дзета-функции Римана, пер. с англ., 1953; [2] Xуa Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [3] Карацуба А. А., «Тр. Матем. ин-та АН СССР», 1971, т. 112, с. 241-55; [4] Марджанишвили К. К., «Докл. АН СССР», 1939, т. 22, с. 391-93; [5] Нооlеу С., «Рrос. London Math. Soc.», ser. 3, 1957, v. 7, № 27, p. 396-413; [6] Линник Ю. В., «Матем. сб.», 1961, т. 53, № 1, с. 3-38; [7] его же, Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [8] Лаврик А. Ф., «Изв. АН СССР. Сер. матем.», 1966, т. 30, № 2, с. 433-48; [9] Виноградов А. И., Линник Ю. В., «Успехи матем. наук», 1957, т. 12, в. 4, с. 277-80; [10] Виноградов А. И., «Изв. АН СССР. Сер. матем.», 1965, т. 29, № 4, с. 903-34.

А. Ф. Лаврик.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.