p-ДЕЛИМАЯ ГРУППА

p-ДЕЛИМАЯ ГРУППА, группа Барсотти-Тейта,- обобщение понятия коммутативной формальной группы. Гомоморфизм, индуцируемый умножением на простое число р, является эпиморфизмом для р-Д. г.

Пусть S - схема, р - простое число; p-делимой группой высоты h наз. индуктивная система G = (G_n, i_n) коммутативных конечных групповых схем G_n порядка р^nh такая, что последовательности

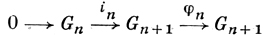
являются точными (здесь φ_n - гомоморфизм умножения на рⁿ). Морфизм р-Д. г. есть морфизм индуктивных систем. р-Д. г. наз. связной (соответственно этальной), если все G_n - связные (этальные) групповые схемы. Связная р-Д. г. над полем характеристики р есть коммутативная формальная группа (рассматриваемая как индуктивный предел ядер φ_n - умножения на рⁿ), для к-рой умножение на р является изогенией [6]. Этот факт обобщается на случай произвольной базисной схемы S, на к-рой гомоморфизм, индуцируемый умножением на р, локально нильпотентен [4]. Категория этальных р-Д. г. эквивалентна категории р-адических представлений фундаментальной группы схемы S. Каждая р-Д. г. G над артиновой схемой S содержит максимальную связную подгруппу G⁰, называемую связной компонентой единицы, фактор по к-рой является этальной р-Д. г. Размерность алгебры Ли для любой (G⁰)_n наз. размерностью р-Д. г. G.

Пусть А - абелево многообразие над полем к размерности d, А(n) - ядро гомоморфизма умножения на рⁿ в A, i_n : А(n) → А (n + 1) - естественное вложение. Индуктивная система А(∞) = (A(n), i_n) является р-Д. г. высоты 2d. Ее связная компонента единицы A(∞)⁰ совпадает с формальным пополнением А вдоль единичного сечения, а высота A(∞)⁰ представляет важный инвариант абелевой схемы.

Пусть G = (G_n, i_n) - р-Д. г. высоты h, Ĝ_n - двойственные по Картье конечные групповые схемы, i_n: Ĝ_n → Ĝ_n+1 - отображение, двойственное к отображению умножения на р : G_n+1 → G_n. Система Ĝ = (Ĝ_n, î_n) является р-Д. г. высоты h и наз. двойственной к р-Д. г. G. Сумма размерностей G и Ĝ равна h.

Как и для формальных групп, для р-Д. г. вводится понятие модуля Дьедонне, играющее важную роль в теории деформации р-Д. г. (см. [2], [3], [4]).

В случае, когда S есть спектр разнохарактеристичес-кого кольца дискретного нормирования А с полем вычетов характеристики р, структура р-Д. г. тесно связана со структурой пополнения алгебраич. замыкания поля частных K кольца A, рассматриваемого как модуль над группой Галуа поля К (см. [6]).

Лит.: [1] Barsotti I., в кн.: Coloque sur la théorie des groupes algébriques tenu à Bruxelles, P., 1962, p. 77-85; [2] Grothendieck А., в кн.: Actes du Congrès international des mathématiciens. 1970, t. 1, P., 1971, p. 431-36; [3] Mazur B., Messing W., Universal Extensions and one Dimensional Crystalline Cohomology, В., 1974; [4] Messing W., The Crystals Associated to Barsotti - Tate Groups: with Applications to Abelian Schemas, В., 1972; [5] Serre J.-P., «Sem. Bourbaki», exposé 318, 1966-67, N. Y., 1968; [6] Тейт Дж., «Математика», 1969, т. 13, № 2, с. 3-25.

И. В. Долгачев.

Источники:

Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.