ДЕКАРТОВ ОВАЛ

ДЕКАРТОВ ОВАЛ - плоская кривая, расстояния r₁ и r₂ каждой точки Р к-рой до двух фиксированных точек F₁ и F₂ (фокусов) связаны неоднородным линейным уравнением

r₁ + mr₂ = a.

Д. о. можно определить при помощи однородного линейного уравнения

r₁ + mr₂ + nr₃ = 0,

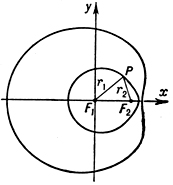
где r₃ - расстояние до третьего фокуса F₃, лежащего на прямой F₁F₂. Д. о. в общем случае состоит из двух замкнутых линий, одна из к-рых объемлет другую (см. рис.). В прямоугольных декартовых координатах уравнение Д. о. имеет вид:

√(x² + y²) + m√((x - d)² + y²) = a,

где d - длина отрезка F₁F₂. При m = 1 и a > d Д. о. представляет собой эллипс, при m = -1 и a < d - гиперболу и, если m = a/d, - Паскаля улитку. Впервые Д. о. исследован Р. Декартом (К. Descartes) в связи с задачами оптики (см. [1]).

Лит.: [1] Декарт Р., Геометрия, пер. [с франц. и латин.], М.-Л., 1938; [2] Савелов А. А., Плоские кривые, М., 1960.

Е. В. Шикин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.