ДЕЙСТВИТЕЛЬНОЕ АЛГЕБРАИЧЕСКОЕ МНОГООБРАЗИЕ

ДЕЙСТВИТЕЛЬНОЕ АЛГЕБРАИЧЕСКОЕ МНОГООБРАЗИЕ - множество A = X(ℝ) действительных точек алгебраич. многообразия X, определенного над полем ℝ действительных чисел. Д. а. м. наз. неособым, если X - неособое алгебраич. многообразие. В этом случае А является гладким многообразием, а его размерность dim А равна размерности комплексного многообразия ℂА = Х(ℂ), называемого комплексификацией многообразия А.

Наиболее изучены неособые регулярные полные пересечения, т. е. многообразия X в проективном пространстве ℝP^q, являющиеся неособыми регулярными пересечениями гиперповерхностей p_i(z) = 0, 1 ≤ i ≤ s, где p_i(z) - однородный действительный многочлен от q переменных степени m_i. В этом случае матрица

||∂p_i/∂z_j||

имеет ранг s в каждой точке z ∈ ℂA; dim A = n = q - s.

Пусть В обозначает Д. а. м., определяемое усеченной системой

p_i(z) = 0, 1 ≤ i ≤ s - 1, p(z) = p_s(z) и m = m_s.

Примеры регулярных полных пересечений:

1) Плоская действительная алгебраич. кривая; при этом q = 2, s = 1, ℂB = ℂР², B=ℝP².

2) Действительная алгебраич. гиперповерхность; при этом s = 1, ℂВ = ℂР^q, B = ℝP^q. В частности, при q = 3 получается действительная алгебраич. поверхность.

3) Действительная алгебраическая пространственная кривая; при этом q = 3, s = 2. Поверхность В задается уравнением p₁(z) = 0, а кривая А высекается на В поверхностью p₂(z) = 0.

Плоская действительная алгебраич. кривая А порядка m₁ состоит в плоскости ℝP² из конечного числа компонент, диффеоморфных окружности. При m₁ четном все они вложены в ℝP² двусторонне, а при m₁ нечетном одна компонента вложена односторонне, а остальные - двусторонне. Двусторонне вложенная компонента кривой А наз. овалом кривой А. Овал, лежащий внутри нечетного числа других овалов кривой А, наз. нечетным, остальные овалы наз. четными.

Число компонент плоской действительной алгебраич.

кривой порядка m₁ не превосходит 1/2 (m₁ - 1){m₂ - 2) + 1 (теорема Гарнака), [1]. Для каждого m₁ существует плоская действительная алгебраич. кривая с этим наибольшим числом компонент - М-кривая (о способах построения M-кривых см. [1], [2], [3], об обобщении этих результатов на пространственные кривые см. [2]). Д. Гильберт (D. Hilbert) в 1900 поставил задачу изучения топологии Д. а. м., а также вложений Д. а. м. в ℝP^q и одного Д. а. м. в другое Д. а. м. (16-я проблема Гильберта). Он указал также трудные частные задачи: изучить взаимное расположение овалов кривой 6-го порядка, топологию и вложение в ℝP³ действительной алгебраич. поверхности 4-го порядка. Эти частные задачи решены (см. [12], [13]).

Для плоской действительной алгебраич. кривой А четного порядка m₁ выполняется точное неравенство

-1/8 (3m²₁ - 6m₁) ≤ P - N ≤ 1/8(3m²₁ - 6m₁) + 1,

где P - число четных овалов кривой А, а N - число ее нечетных овалов (теорема Петровского).

Если m₁ нечетно, то аналогичное неравенство выполнено для A ∪ L, где L - прямая в общем положении [4]. При обобщении этих результатов на случай действительной алгебраич. гиперповерхности четного порядка роль разности Р - N играет эйлерова характеристика χ(В₊), где В₊ = {z ∈ B|p(z) ≥ 0}, если же q нечетно, то роль Р - N играет χ(А). Так, для действительной алгебраич. гиперповерхности А четного порядка m₁

|χ(B₊)| ≤ 1/2 (m₁ - 1)^q - s(q; m₁) + 1/2,

где s(q; m₁) - число членов многочлена

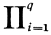 (1 + x_i + ... + x^m-2_i),

степень которых не превосходит 1/2(qm₁ - 2q - m₁); при нечетном q и любом m₁

|χ(A)| ≤ (m₁ - 1)^q - 2s(q; m₁) + 1

(см. [5]). Для действительной алгебраической пространственной кривой (в ℝP³) при четном m₁ выполняется неравенство

|χ(B₊)| ≤ 1/3 m³₁ + 3/8 m₁m²₂ + 1/4 m²₁m₂ - m²₁ - m₁m₂ + 7/6 m₁ + |χ(B)|/2

(в случае m₁ = 2 эта оценка точная) (см. [6]). Имеются обобщения теорем Петровского на произвольные Д. а. м. (см. [10]).

Для плоской действительной алгебраич. М-кривой четного порядка m₁ выполняется сравнение

P - N ≡ (m₁/2)² mod 8

(см. [8], [9], [13]). При доказательстве этого сравнения (см. [8], [9]) были применены для изучения Д. а. м. методы дифференциальной топологии, в форме стимулирующей дальнейшие исследования. Пусть плоская действительная алгебраич. кривая А имеет четный порядок m = 2k, знак перед p(z) выбран так, что В₊ ориентируемо, а Р₊, Р₀, Р_- обозначают соответственно число овалов кривой А, ограничивающих внешним образом компоненту множества В₊ с положительной, нулевой и отрицательной эйлеровыми характеристиками. Аналогично, N₊, N₀, N_- - числа таких же нечетных овалов для В_- = {z ∈ B | p(z) ≤ 0}. Тогда (см. [8], [13])

P_- + P₀ ≤ 1/2 (k - 1)(k - 2) + E(k),

N_- + N₀ ≤ 1/2 (k - 1)(k - 2),

P_- ≥ N - 3/2 k(k - 1),

N_- ≥ P - 3/2 k(k - 1),

где

E(k) = 1/2 (l + (-1)^k).

Для произвольного Д. а. м. в q-мерном проективном пространстве выполнено неравенство

dim H_* (А; ℤ₂) ≤ dim H_*(ℂA; ℤ₂),

где Н_*(А; ℤ₂) = ∑(A, ℤ₂) - пространство гомологии многообразия А с коэффициентами в ℤ₂ (см. [9]). Это неравенство является обобщением теоремы Гарнака. Если

dim H_*(ℂA; ℤ₂) - dim H_*(A, ℤ₂) = 2t

(t всегда целое), то А наз. (М - t)-многообразием. При t = 0 А есть M-многообразие.

Доказаны следующие сравнения:

A) Для М-многообразия А при четном n

χ(A) ≡ σ(ℂA)mod 16,

где σ(ℂА) - сигнатура многообразия ℂА (см. [9]).

B) Для (М-1)-многообразия А при четном n

χ(А) ≡ σ(ℂА) ± 2 mod 16

(см. обзор [13]).

C) В случае регулярного полного пересечения, если n четно, А есть (М - 1)-многообразие и гомоморфизм включения

i_*: H_n/2 (A, ℤ₂) → N_n/2(ℝP^q; ℤ₂)

нулевой, то

d = m₁m₂ ... m_s = 2 mod 4

и

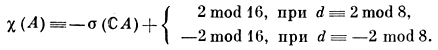
В этом же случае, если n четно, А есть (М - 2)-много-образие и i_* - нулевой, то

при d ≡ 0 mod 8, χ(А) ≡ ±σ(ℂA) mod 16, при d ≡ 2 mod 8, χ(A) ≡ -σ(ℂА) + 4 mod 16,

или χ(A) ≡ ± σ(ℂA) mod 16, при d - 2 mod 8, χ(А) ≡ -σ(ℂА) - 4 mod 16,

или χ(А) ≡ ±σ(ℂA) mod 16

(см. [11]).

В частности, для действительной алгебраич. поверхности А порядка m₁

dim H_*(ℂA; ℤ₂) = m³₁ - 4m²₁ + 6m₁, если А есть M-поверхность, то

χ(A) ≡ 1/3 (4m₁ - m³₁) mod 16;

если A есть (М-1)-поверхность, то

χ(A) ≡ 1/3(4m₁ - m³₁) ± 2 mod 16;

если A есть (М-1)-поверхность и стягивается в ℝP³ в точку, то m₁ = 2 mod 4 и

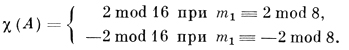
Если A есть (М-2)-поверхность и стягивается в ℝ'P³ в точку, то

Доказаны также нек-рые сравнения при нечетном п (см. [9], [13]). В частности, для плоской действительной алгебраич. кривой A, являющейся (М-1)-кривой четного порядка m₁:

P - N ≡ (m₁/2)² ± 1 mod 8.

Имеются некоторые результаты о Д. а. м. с особенностями (см. обзор [13]). Интересный подход к изучению Д. а. м. предложен в [14].

Лит.: [1] Наrnасk А., «Math. Ann.», 1876, Bd 10, S. 189-99; [2] Hilbert D., там же, 1891, Bd 38, S. 115-38; [3] eго жe, «Arch. Math. Phys.» (3), 1901, Bd 1, S. 213-37; [4] Петровский И. Г., «Ann. Math.», 1938, v. 39, № 1, p. 189-209; [5] Олeйник О. А., Петровский И. Г., «Изв. АН СССР. Сер. матем.», 1949, т. 13, с. 389-402; [6] Олейник О. А., «Матем. сб.», 1951, т. 29, с. 133-56; [7] Проблемы Гильберта, М., 1969; [8] Арнольд В. И., «Функциональный анализ», 1971, т. 5, № 3, с. 1-9; [9] Рохлин В. А., там же, 1972, т. 6, № 4, с. 58-64; 1973, т. 7, № 2, с. 91-92; [10] Харламов В. М., «Функциональный анализ», 1974; т. 8, №2, с. 50-56; 1975, т. 9, № 3, с. 93-94; [11] его же, там же, 1975, т. 9, № 2, с. 51-60; [12] его же, там же, 1976, т. 10, № 4, с. 55-68; [13] Гудков Д. А., «Успехи матем. наук», 1974, т. 29, в. 4, с. 3-79; [14] Сулливан Д., Геометрическая топология, пер. с англ., М., 1975.

Д. А. Гудков.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.