ДЕЙСТВИЕ

ДЕЙСТВИЕ - функционал, выражаемый определенным интегралом от функции, стационарные значения к-рого определяют действительное движение механич. системы под действием заданных активных сил в классе кинематически возможных движений, удовлетворяющих определенным условиям, между нек-рыми двумя конечными положениями Р₀ и Р₁ в пространстве.

Различают Д. по Гамильтону, Лагранжу и Якоби, фигурирующие в соответствующих принципах стационарного действия.

Д. по Гамильтону:

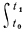 (T + U)dt.

определено в классе кинематически возможных движений голономной системы, для к-рых начальное и конечное положения системы и время движения между ними одинаковы с таковыми для действительного движения.

Д. по Лагранжу:

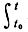 2T dt,

Д. по Якоби:

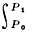 √(2(U + h)) ds,

ds² = 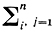a_ij dq_i dq_j,

определены в классе кинематически возможных движений голономной консервативной системы, для к-рых начальное и конечное положения системы и постоянная энергия h одинаковы с таковыми для действительного движения. Здесь Т - кинетич. энергия системы, причем для консервативной системы

T = 1/2 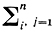a_ijq̇_iq̇_j,

где q̇_i - обобщенные лагранжевы координаты, U(q) силовая функция активных сил.

Подробнее см. Вариационные принципы классической механики, а также Гамильтона - Остроградского принцип, Лагранжа принцип, Якоби принцип.

В. В. Румянцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.