ДЕВЯТИ ТОЧЕК ОКРУЖНОСТЬ

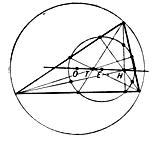
ДЕВЯТИ ТОЧЕК ОКРУЖНОСТЬ, окружность Эйлера,- окружность, на к-рой расположены середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр треугольника с вершинами. Ее радиус равен половине радиуса окружности, описанной около треугольника. Д. т. о. треугольника касается вписанной в него окружности и трех вневписанных окружностей. Пусть Н - ортоцентр неравностороннего треугольника, Т - центр тяжести, О - центр описанной окружности, Е - центр Д. т. о. Точки Н, Т, О, Е лежат на одной прямой (прямая Эйлера), причем Е - середина отрезка НО и пара точек Н, Т гармонически разделяет пару точек О, Е.

Лит.: [1] Зетель С. И., Новая геометрия треугольника, 2 изд., М., 1962; [2] Перепелкин Д. И., Курс элементарной геометрии, ч. 1, М.-Л., 1948.

В. Т. Базылев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.