ДВУСТОРОННЯЯ ОЦЕНКА

ДВУСТОРОННЯЯ ОЦЕНКА - совокупность оценок некоторой величины а сверху и снизу. Оценкой сверху наз. неравенство вида a ≤ A₁ оценкой снизу - неравенство противоположного смысла а ≥ A₀. Величины А_{0/sub>, A1/, c помощью к-рых оценивается величина а, как правило, имеют или более простой вид или значительно легче вычисляются чем a.}

Примеры. 1) Пусть m, М - соответственно наименьшее и наибольшее значения функции f(х) на отрезке [α, β]; тогда для интеграла 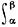f(x)dx справедлива Д. о.:

m(β - α) ≤ 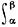f(х)dx ≤ М(β - α),

где

A₀ = m(β - α), a = 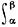f(x)dx, A₁ = М(β - α).

2) Д. о. констант Лебега L_n при всех n = 0, 1, 2, ...:

0,9897 ... < L_n - 4/π² ln(2n + 1) ≤ 1.

3) Д. о. собственных значений. Пусть поставлена задача на собственные значения линейного самосопряженного оператора Т : Тu = λu в гильбертовом пространстве Н. Строится следующий итерационный процесс: Tf_n+1 = f_n, где f₀ ≠ 0. В силу самосопряженности оператора Т скалярные произведения (f_m, f_k) зависят лишь от суммы индексов m + k. Числа а_n = (f₀, f_n) = (f_n, f_n) наз. постоянными Шварца, а числа μ_n+1 = а_n/а_n+1 - частными Рэлея-Шварца. Если оператор Т положительный, то μ_n образуют монотонную невозрастающую сходящуюся последовательность.

Если λ₀ - собственное значение оператора Т, а < λ₀ < < b, a < μ_2k < b, и на интервале (а, b) нет других точек спектра оператора T, то

μ_2k - ρ² / (b - μ_2k) ≤ λ₀ ≤ μ_2k + ρ² / (μ_2k - a), ρ² = (μ_2k-1 - μ_2k) / μ_2k

(теорема Темпля [3]). При определенных условиях частные Рэлея-Шварца сходятся к нек-рому собственному значению оператора Т.

Численные методы получения Д. о. (двусторонних приближений) наз. двусторонними методами [4]. Рассмотренный выше способ построения частных Рэлея-Шварца является примером двустороннего метода. Нек-рые двусторонние методы основаны на использовании пары приближенных формул, имеющих остаточные члены противоположных знаков. Пусть, напр., функция f(x), заданная в точках (узлах интерполяции) x₀ < ₁ < ... < x_n интерполируется многочленом Лагранжа L₀(x) с узлами х₀, x₁, ..., x_n-1, L₁(х) - интерполяционный многочлен Лагранжа с узлами x₁, x₂, ..., x_n. Тогда для остаточных членов справедливы соотношения:

R₀(x) = f(x) - L₀(x) = f⁽ⁿ⁾(ξ₀) / n! (х - х₀)(x - x₁) ... (x - x_n-1), R₁(x) = f(x) - L₁(x) = f⁽ⁿ⁾(ξ₁) / n! (х - х₁)(x - x₂) ... (x - x_n),

где ξ₀, ξ₁ ∈ [x₀, х_n]. Если производная f⁽ⁿ⁾(x) не меняет знака на отрезке [x₀, х_n], то R₀(x) и R₁(х) имеют разные знаки. Справедлива Д. о.:

min(L₀(x), L₁(x)) ≤ f(x) ≤ max(L₀(x), L₁(х)).

Наиболее разработаны двусторонние методы решения обыкновенных дифференциальных уравнений [5] - [9].

Двусторонние методы дают возможность указать границы области, в к-рой заведомо лежит решение задачи. При этом приходится согласиться с усложнением алгоритма. Более того, чтобы обеспечить двусторонность в реальных вычислениях (при наличии ошибок округлений), приходится еще более усложнять алгоритм. Двусторонние методы применяются в основном в тех случаях, когда необходимо иметь гарантированную оценку погрешности.

Лит.: [1] Галкин П. В., «Тр. Матем. ин-та АН СССР», 1971, т. 109, с. 3-5; [2] Коллатц Л., Задачи на собственные значения с техническими приложениями, пер. с нем., М., 1968; [3] его же, Функциональный анализ и вычислительная математика, пер. с нем., М., 1969; [4] Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [5] Волков Е. А., «Тр. Матем. ин-та АН СССР», 1971, т. 112, с. 141-51; [6] Ремез Е. Я., «Зап. природниго-техiчного вiддiлу» АН УССР, 1931, № 1, с. 1-38; [7] Горбунов А. Д., Шахов Ю. А., «Ж. вычисл. матем. и матем. физ.», 1963, т. 3, № 2, 239-53; 1964, т. 6, № 3, 426-33; [8] Девятко В. И., там же, 1963, т. 3, № 2, 254-65; [9] Салихов Н. П., там же, 1962, т. 2, № 4, 515-28.

В. В. Поспелов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.