ДВУМЕРНОЕ МНОГООБРАЗИЕ

ДВУМЕРНОЕ МНОГООБРАЗИЕ - топологическое пространство, каждая точка к-рого обладает окрестностью, гомеоморфной плоскости или полуплоскости. Д. м. - наиболее наглядный класс многообразий: к ним относятся сфера, круг, лист Мёбиуса, проективная плоскость, бутылка Клейна и др.

Точки, имеющие лишь такие окрестности, к-рые гомеоморфны полуплоскости (если они есть), образуют край многообразия.

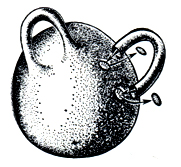
Рис. 1.

Важнейший класс Д. м. составляют замкнутые ориентируемые Д. м., или замкнутые поверхности. Простейшая из них - сфера S² - поверхность рода 0. Поверхность рода g получается из S² удалением 2g пар непересекающихся дисков и отождествлением с каждой парой граничных окружностей границ изогнутого цилиндра (рис. 1). Этот процесс наз. приклеиванием ручек, а замкнутая поверхность рода g - сферой с g ручками (рис. 2).

Рис. 2.

Более широкий класс Д. м. составляют компактные ориентируемые Д. м., или поверхности с краем, получаемые из к.-л. замкнутой поверхности удалением внутренних точек конечного числа непересекающихся дисков. Их границы образуют край возникающего Д. м. Родом этого Д. м. считается род исходной поверхности (рис. 3). Д. м. рода 0 - диск или диск с дырами.

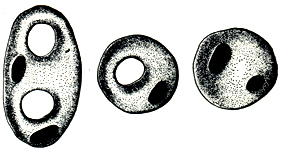
Рис. 3.

В другой класс Д. м. входят компактные неориентируемые Д. м. Они также могут быть замкнутыми и с краем. Простейшее среди них - Мёбиуса лист (рис. 4). Он не может быть ориентирован, т. е. на нем нельзя выбрать одновременно для каждой точки направления вращения вокруг нее так, чтобы эти направления переходили друг в друга непрерывно. Другой пример - проективная плоскость ℝP²; любая окрестность каждой проективной прямой на ℝP²; содержит лист Мёбиуса и поэтому ℝP²; также неориентируема. В общем случае компактные неориентируемые Д. м. получаются из замкнутых поверхностей удалением внутренних точек непересекающихся дисков и заклейкой их (не обязательно каждого) листами Мёбиуса (на рис. 5 лист Мёбиуса представлен в виде скрещенной крышки, т. е. с самопересечением по отрезку). Проективная плоскость ℝP²; получается из сферы заменой одного диска на лист Мёбиуса. Если заменить листами Мёбиуса два диска, то получится Клейна поверхность (рис. 6), ее удобно изображать также как сферу с неориентируемой ручкой. Вообще, приклейку двух листов Мёбиуса можно заменить приклейкой одной неориентируемой ручки, и наоборот. С другой стороны, если обвести один конец обычной ручки по средней линии листа Мёбиуса, то эта ручка станет неориентируемой (рис. 7). Таким образом, в неориентируемом Д. м. любую ручку можно заменить на два листа Мёбиуса, и наоборот.

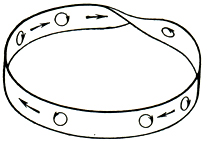
Рис. 4.

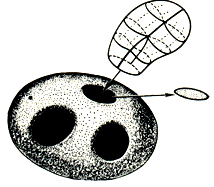
Рис. 5.

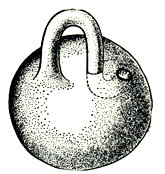
Рис. 6.

Сферами с ручками или с листами Мёбиуса и, возможно, с удаленными дисками исчерпываются все компактные связные (состоящие из одного куска) Д. м. Некомпактные Д. м., напр. плоскость ℝ², полуплоскость ℝ²₊ и вообще любое открытое подмножество любого компактного Д. м., могут быть очень сложно устроены. Напр., если на ℝ² взять бесконечное число дисков, уходящих на бесконечность, и заменить их на ручки или листы Мёбиуса, то получится Д. м., к-рое не является открытым подмножеством никакого компактного Д. м. (рис. 8). Некомпактные Д. м. без края наз. открытыми.

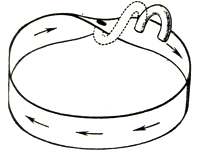
Рис. 7.

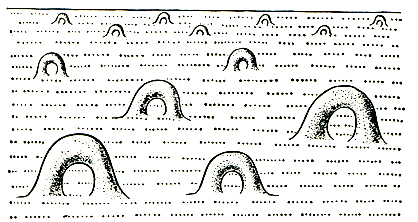
Рис. 8.

Одним из подходов к изучению Д. м. является комбинаторный подход, при к-ром Д. м. рассматривается состоящим из выпуклых многоугольников (граней), примыкающих друг к другу по общим ребрам. Особенно важны триангуляции Д. м., где гранями являются треугольники. Если два Д. м. триангулированы, то их триангуляции наз. комбинаторно эквивалентными, когда они имеют изоморфные подразделения, между элементами которых можно установить взаимно однозначное соответствие, сохраняющее примыкание соответствующих граней. Из произвольных двумерных комплексов триангулированные Д. м. выделяются тем, что к каждому ребру примыкают одна (для ребер на краю) или две грани и вокруг каждой вершины триангуляции грани образуют один цикл (звезду) последовательно примыкающих друг к другу граней (рис. 9). Цикл замкнут, если вершина не лежит на краю (а), и незамкнут, если она лежит там (Ь). Компактность Д. м. равносильна конечности числа граней любой триангуляции, а связность - возможности соединить любые две вершины цепочкой ребер. В связном Д. м. любые две грани соединимы цепочкой граней, в к-рой две соседние имеют общее ребро. Неориентируемость равносильна существованию такой цепочки, к-рая содержит в себе лист Мёбиуса.

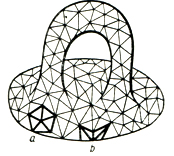
Рис. 9.

С помощью триангуляции удобно вводить инварианты, т. е. характеристики, одинаковые у комбинаторно эквивалентных Д. м. Важнейшим инвариантом является эйлерова характеристика χ(М), равная для данной триангуляции числу В - P + Г, где В, Р, Г -числа вершин, ребер и граней триангуляции соответственно. χ не меняется при подразделениях, и поэтому если χ(М₁) ≠ χ(М₁), то М₁ и М₂ комбинаторно неэквивалентны. Для сферы с g ручками χ(М) = 2 - 2g, в частности для сферы она равна 2, для тора 0, для проективной плоскости 1, для бутылки Клейна 0, для сферы с к листами Мёбиуса 2 - k. Если из Д. м. выбросить внутренности k дисков, то χ(М) уменьшится на k. Сопоставляя компактному связному Д. м. три числа

{ε, χ, k},

где ε = ±1 в зависимости от ориентируемости, χ = χ(М), а k - число компонент края, получаем тем самым полное описание Д. м. с точностью до комбинаторной эквивалентности, поскольку эти тройки чисел различны для описанных выше Д. м. (сфер с ручками, сфер с листами Мёбиуса и, возможно, еще с дырами), и в то же время любое компактное связное Д. м. комбинаторно эквивалентно одному из этих Д. м. (см. [1], [3]). Для открытых Д. м. классификация также проведена, но она здесь гораздо сложнее, так как имеется несчетно много различных поверхностей [5].

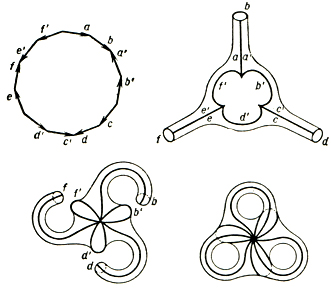
Рис. 10.

Для чисто топологич. изучения Д. м. основную роль играет Жордана теорема. Пусть С - кривая без самопересечений, соединяющая две точки края многообразия М или замкнутая; она называется сечением М. Сечение С не разбивает М, если любые две точки М соединимы дугой, не пересекающей С. Максимальное число сечений, к-рые вместе не разбивают М, увеличенное на единицу, наз. числом связности М. Так, согласно теореме Жордана, сфера и диск односвязны. Связность замкнутой поверхности рода g равна 2g + 1 = = 3 - χ. Для такой поверхности имеется набор из 2g сечений, к-рые все выходят из одной точки и разбиваются на пары так, что каждая пара осуществляет разрез одной ручки. Такой набор наз. каноническим разрезом М: в результате разрезания по всем сечениям М превращается в диск. Аналогично имеются канонич. разрезы неориентируемых Д. м. (по средним линиям листов Мёбиуса). Для Д. м. с краем нужно провести еще сечения из базисной точки к каждой компоненте края. Обратно, Д. м. возникает из диска, край к-рого разбит на сегменты, склеиванием этих сегментов попарно между собой. Если склеивание осуществляется по схеме рис. 10, то получается ориентируемое Д. м., если по схеме рис. 11, то - неориентируемое. (Сегмент x надо склеить с сегментом х' так, чтобы совпали направления стрелок.) Край возникает, если имеется несколько сегментов, по к-рым не производится склейки.

Теорема Жордана позволяет также дать топологич. характеризацию Д. м. В частности, сфера есть единственный локально связный континуум, содержащий топологич. образ окружности, разбиваемый каждым образом окружности и не разбиваемый никакой парой точек. Вообще, Д. м. выделяются в классе локально связных континуумов тем, что они не разбиваются никакой парой точек и разбиваются достаточно малой окружностью (теорема Уайлдера, 1949).

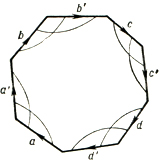
Рис. 11.

Поскольку у гомеоморфных Д. м. любые две триангуляции комбинаторно эквивалентны, комбинаторная классификация Д. м. имеет чисто топологич. смысл. Хотя набором е, у, к компактные Д. м. характеризуются однозначно, для изучения свойств Д. м. имеют значение и другие топологич. инварианты. В первую очередь это - одномерных гомологии группа Н₁(М) и фундаментальная группа π₁(М). Для замкнутой поверхности рода g H₁(М) равна прямой сумме 2g экземпляров группы ℤ целых чисел. В качестве образующих обычно берутся g пар окружностей канонич. разреза. Для неориентируемого замкнутого Д. м. с числом связности s Н₁(М) есть сумма s - 1 экземпляров группы ℤ и одного экземпляра группы ℤ₂. За образующие берутся сечения канонич. разреза (за вычетом одного) и еще дезориентирующий путь (после разреза по которому Д. м. становится ориентируемым). Для π₁(М) копредставление удобнее всего получается с помощью канонического разреза: его сечения берутся за образующие, а соотношение получается при обходе края диска, возникшего после разреза. В ориентируемом случае получается копредставление

{ a₁, b₁; ..., a_g, b_g; a₁b₁a^-1₁b^-1₁ ... a_gb_ga^-1_gb^-1_g = 1},

а в неориентируемом

{ a₁, ..., a_s; a²₁a²₂ ... a²_s = 1 }.

Имеет значение тот факт, что универсальным накрытием любого связного Д. м. без края (кроме s² и ℝP²) является плоскость ℝ², а соответствующая монодромии группа реализуется движениями евклидовой плоскости или плоскости Лобачевского. Напр., тор получается отождествлением всех точек плоскости, отличающихся друг от друга на mv₁ + nv₂, где v₁ и v₂ - два данных вектора, а m и n - целые числа. Для применений важны также и накрытия с ветвлением. Пусть отображение f : М₁ → М₂, где М₁ и М₂ - замкнутые и триангулированные Д. м., линейно отображают каждую грань М₁ на некоторую грань М₂, причем для каждого ребра l в М₁ примыкающие к нему две грани отображаются на разные грани, примыкающие к ребру f(l) в М₂. Для каждой точки х ∈ М₁, отличной от вершин, найдется в М₁ окрестность, к-рую f переводит взаимно однозначно на окрестность точки f(x) в М₂. Если для вершины v из М₁ обойти в циклич. порядке примыкающие к ней грани, то соответствующие грани в М₂ обойдут в циклич. порядке вершину f(v) в М₂ целое число k раз. Если k=1, то v - обыкновенная точка, если же k > 1, то v - точка ветвления, а k - кратность ветвления в точке v. Если f^-1(w) для w ∈ M₂ не содержит точек ветвления, то w также наз. обыкновенной. Поскольку прообразы близких обыкновенных точек из М₂ состоят из равного числа точек, по соображениям непрерывности получается, что это число - одно и то же для всех обыкновенных точек. Оно наз. числом листов накрытия. Это число d равно для ориентируемого Д. м. степени отображения f (в случае неориентируемости его следует привести по модулю два). Если f^-1(w) содержит точки ветвления с кратностями k₁, ..., k_t, то f^-1(w) содержит на ∑(k_i - 1) меньше точек, чем обыкновенная точка (здесь суммирование по всем точкам ветвления в М₁). Поскольку число вершин В(М₁) на ∑(k_i - 1) меньше d ⋅ B(M₂), а для числа ребер и граней: Р(М₁) = d ⋅ P(M₂) и P(М₁) = d ⋅ P(M₂), то

χ(M₁) = d ⋅ χ(M₂) - ∑(k_i - 1).

Это - формула Римана-Гурвица.

С точки зрения дифференциальной геометрии Д. м. рассматриваются как гладкие многообразия, к-рые снабжаются дополнительными структурами (напр., метрикой, связностью и т. д.) или рассматриваются вложенными (с возможными самопересечениями) в евклидовы пространства. Гладкое Д. м. можно триангулировать так, что ребра будут гладкими дугами, а все углы отличны от нуля (теорема Керне а, 1934). Оказывается, что при этом диффеоморфным Д. м. отвечают комбинаторно эквивалентные триангуляции, и обратно. Таким образом, классификация Д. м. сохраняет силу и для гладких Д. м. Примером теоремы, связывающей топологич. характеристики Д. м. с его дифференциально-геометрич. свойствами, является теорема Гаусса - Бонне [3]: интеграл от кривизны замкнутой поверхности (точнее, от гауссовой кривизны, определяемой нек-рой римановой связностью, к-рую всегда можно определить на гладком Д. м.) равен 2πχ(М). Этот факт, а также его интерпретация с помощью так наз. гауссова отображения (в частности, сферического отображения) в многообразие Грассмана, если рассматриваемое многообразие погружено в евклидово пространство, находит обобщение в теории характеристических классов. Другая теорема, также послужившая одним из истоков этой теории: сумма индексов особых точек любого векторного поля на замкнутой поверхности равна χ(М).

Важную роль Д. м. играют в теории функции комплексного переменного. Здесь Д. м. наделяются комплексными структурами, т. е. локальными параметризациями окрестностей точек, связанными между собой аналитич. функциями, и наз. римановыми поверхностями [4]. Они обязательно ориентируемы. Замкнутые римановы поверхности являются геометрич. моделями комплексных алгебраических кривых. Комплексное строение на Д. м. не определяется однозначно его дифференциально-топологич. строением: напр., на поверхности рода g комплексные структуры образуют континуум размерности 6g-6 (теорема Тейхмюллера, 1940).

К определению Д. м. иногда добавляются требования, чтобы оно как топологич. пространство было хаусдорфовым или имело счетную базу (последнее, в частности, необходимо для триангулируемости Д. м.: существуют хаусдорфовы нетриангулируемые Д. м., см. Прюфера поверхность).

Лит.: [1] Александров П. С., Ефремович В. А., Очерк основных понятий топологии, М.-Л., 1936; [2] Гильберт Д., Кон-Фоссен С, Наглядная геометрия, пер. с нем., 2 изд., М.-Л., 1951; [3] Бакельман И. Я., Вернер А. Л., Кантор Б. Е., Введение в дифференциальную геометрию «в целом», М., 1973; [4] Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [5] Стоилов С., Лекции о топологических принципах теории аналитических функций, пер. С франц., М., 1964.

А. В. Чернавский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.