ДВУЖИДКОСТНАЯ МОДЕЛЬ ПЛАЗМЫ

ДВУЖИДКОСТНАЯ МОДЕЛЬ ПЛАЗМЫ - гидродинамическая модель, в к-рой плазма рассматривается как совокупность двух «жидкостей» (электронной и ионной), движущихся одна сквозь другую. Электрич. сопротивление плазмы рассматривается как результат взаимного трения этих жидкостей.

Система уравнений движения в предположении, что на электроны действует только электронное давление р_e, а на ионы - лишь ионное давление p_i, имеет вид

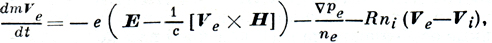
(1)

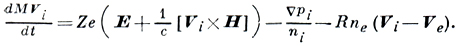
(2)

Взаимодействие электронов и ионов учтено посредством силы трения, пропорциональной произведению разности скоростей на концентрацию тормозящих частиц. Величина R наз. коэффициентом взаимного трения, или коэффициентом диффузионного сопротивления. Учитывая условие квазинейтральности плазмы (n_e = zn_i = n), уравнение движения Д. м. п. приводится к виду

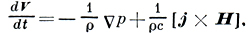
где

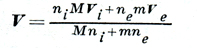
- средняя массовая скорость, p = p_i + p_e - суммарное давление, a j = e(Zn_iZ_i - n_eZ_e) - ионный ток. Если m/M ≪ 1, то V_i ≈ V, V_e ≈ V - jne.

Уравнения (1), (2) могут быть использованы для получения обобщенного закона Ома, связывающего плотность тока j с другими величинами. Если можно пренебречь членами вида (V∇)V (а также при m/М ≪ 1), обобщенный закон Ома записывается в виде:

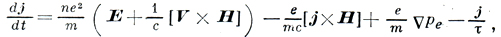
где τ = 1/χ_eⁱ - так наз. время передачи импульса, χ_eⁱ - эффективная частота передачи импульса, определяемая выражением:

R = m/n_i χ_eⁱ = m/n_e χ_i^e.

Лит.: [1] Франк-Каменецкий Д. А., Лекции по физике плазмы, 2 изд., М., 1968; [2] Куликовский А. Г., Любимов Г. А., Магнитная гидродинамика, М., 1962.

В. А. Дородницын.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.