S-ДВОЙСТВЕННОСТЬ

S-ДВОЙСТВЕННОСТЬ, стационарная

двойственность, Спеньера двойственность, - двойственность в теории гомотопии, имеющая место (при отсутствии ограничений на размерность пространств) для аналогов обычных гомотопич. и когомотопич. групп в надстроечной категории - для S-гомотопич. и S-когомотопич. групп или стационарных групп гомотопий и когомотопий, образующих экстраординарные (обобщенные) теории гомологии и когомологий. Надстроечной категорией, или S-категорией, наз. категория, объектами к-рой являются топологич. пространства X, а морфизмами - классы {f} S-гомотопных отображений f p-кратной надстройки S^pX₁ в S^pX₂, причем f и g: S^qX₁ → S^qX₂ считаются S-гомотопными, если существует такое r ≥ max(p, q), что надстройки S^r-pf S^r-pg гомотопны в обычном смысле. Множество {Х₁, Х₂} таких классов, наз. S-oтображениями, составляет абелеву группу (относительно так наз. колейного сложения, см. [1], [2], [4], [5]). Группа {Х₁, Х₂} есть предел прямого спектра множеств [S^kХ₁, S^kХ₂] обычных гомотопич. классов с надстроечными отображениями в качестве проекций, являющегося при достаточно больших к спектром групп с гомоморфизмами. Имеет место изоморфизм S : {Х₁, Х₂} → {SХ₁, SХ₂}, при к-ром соответствующие друг другу элементы представляются одним и тем же отображением S^pX₁ → S^pX₂, p ≥ 1. Полиэдром, n-двойственным к полиэдру X сферы Sⁿ, наз. произвольный полиэдр D_nХ в Sⁿ, являющийся S-деформационным ретрактом дополнения Sⁿ\X, т. е. если морфизм, соответствующий вложению D_nX ⊂ Sⁿ\X, есть S-эквивалентность. Полиэдр D_nХ существует для каждого X, и можно рассматривать X как D²_nX.

Для любых полиэдров Х₁, Х₂ и любых n-двойственных им полиэдров D_nX₁ и D_nX₂ существует единственное отображение

D_n: {X₁, X₂} → {D_nX₂, D_nX₁},

удовлетворяющее следующим условиям:

а) Оно является инволютивным контравариантным функториальным изоморфизмом, т. е. D_n есть такой гомоморфизм, что если

i : Х₁ ⊂ Х₂ и i' : D_nX₂ ⊂ D_nX₁

то

D_n{i) = {i'};

если

{f₁} ∈ {X₁, X₂} и {f₂} ∈ {X₂, X₃}

то

D_n({f₂}⋅{f₁}) = D_n{f₁} ⋅ D_n(f₂);

если θ - элемент из {Х₁, Х₂} или из {D_nX₂, D_nX₁}, то D_nD_nθ = θ.

б) Оно удовлетворяет соотношениям

SD_n = D_n+1 и D_n+1S = D_n,

где SD_nX_j и D_nX_i рассматриваются как полиэдры, (n+1)-двойственные к полиэдрам X_i и, соответственно, SX_i, i = 1, 2; это значит, что оно не зависит от n и стационарно относительно надстройки.

в) Оно удовлетворяет равенству

Dⁿ_aθ_* = {D_nθ)^*Dⁿ_a, где

θ_*: H_p(X₁) → H_p(X₂)

и

(D_nθ)^* : H^n-p-1(D_nX₁) → H^n-p-1(D_nX₂)

- гомоморфизмы указанных групп гомологии и когомологии, индуцированные S-отображениями θ ∈ {Х₁, Х₂} и D_nθ, а

D_a : Н_p(Х_i) → H^n-p-1(D_nX_i), i = 1, 2, есть изоморфизм, к-рый получается из изоморфизма Александера двойственности заменой множества Sⁿ\X_i его S-деформационным ретрактом D_nX_i.

Построение D_n опирается на представление данного отображения как композиции вложения и S-деформационной ретракции.

S-гомотопической группой Σ_p(Х) пространства X наз. группа {S^p, X}, а S-когомотопической группой Σ^p(Х) пространства X - группа {X, S^p}. Как и в обычной теории гомотопии, определяются гомоморфизмы

φ_p : Σ_p(X) → H_p(X),

φ^p : Σ^p(X) → H^p(X).

Рассмотрение сфер S^p и S^n-p-1 как n-двойственных приводит к изоморфизму

D_n: Σ_p(X) → Σ^n-p-1(D_nX) и к коммутативной диаграмме

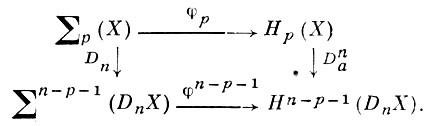
Таким образом, изоморфизм D_n связывает S-гомотопич. и S-когомотопич. группы подобно тому, как изоморфизм двойственности Александера Dⁿ_a связывает группы гомологии и когомологии. Какая-либо двойственность в S-категории приводит к двойственности в случае обычных гомотопич. классов, если на пространство наложить требования, из к-рых следует наличие взаимно однозначного соответствия множества указанных классов с множеством S-гомотопических классов.

Примерами двойственных предложений в этой теории являются теорема Гуревича об изоморфизме и теорема классификации Хопфа. D_n переводит одну из этих теорем в другую, что означает замену S-гомотопич. групп S-когомотопическими, групп гомологии - группами когомологии, отображения φ_p - отображениями φ^n-p-1, наименьшей размерности с нетривиальной гомологич. группой - наивысшей размерностью с нетривиальной группой когомологии, и наоборот. В обычной теории гомотопии для определения n-когомотопич. группы требуется, чтобы размерность пространства не превышала 2n - 2 (или, более общо, чтобы пространство было (2n - 1)-косвязным, n > 1), что нарушает полную общность двойственности.

Теория обобщается в различных направлениях: напр., рассматриваются пространства, имеющие S-гомотопи-ческий тип полиэдров, относительный случай, теория с носителями и др. (см. [3], [5], [6], [7]). Она послужила одним из источников стационарной гомотопической теории [8].

Лит.: [1] Спаньер Э. Г., «Математика», 1959, т. 3, № 1, с. 17-25; [2] Sрaniеr Е. Н., Whitehead J. Н. С., «Mathematica», 1955, v. 2, № 3, p. 56-80; [3] их же, «Аnn. Math.», 1958, v. 67, № 2, p. 203-38; [4] Barratt M. G., «Рrоc. Lond. Math. Soc.», 1955, v. 5, p. 71 - 106, 285 - 329; [5] Спаньер Э. Г., Уайтхсд Дж. Г., «Математика», 1959, т. № 1, с. 27-56; [6] Экман В., Хилтон П., там же, 1960 т. 4, № 3, с. 3-27; [7] Спаньер Э., Алгебраическая топология, пер. с англ., М., 1971; [8] Уайтхед Дж., Новейшие достижения в теории гомотопий, пер. с англ., М., 1974.

Г. С. Чогошвили.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.