ДВОЙСТВЕННОСТЬ

ДВОЙСТВЕННОСТЬ - 1) Д. в алгебраической геометрии - двойственность между различными пространствами когомологий на алгебраич. многообразиях.

Когомологии когерентных пучков. Пусть X - неособое проективное алгебраич. многообразие размерности n над алгебраически замкнутым полем k, a ℒ - локально свободный пучок на X. Теорема двойственности Серра утверждает, что конечномерные линейные векторные пространства когомологий Нⁱ(Х, ℒ) и H^n-i(X, ℒ̆ ⊗ ω_X) двойственны друг другу. Здесь ω_X = Ωⁿ_X - пучок ростков регулярных дифференциальных форм n-й степени на X, a 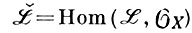- двойственный к ℒ локально свободный пучок. В случае, когда 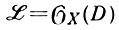- обратимый пучок, соответствующий дивизору D на X, эта теорема устанавливает равенство

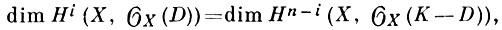
где К - канонич. дивизор на X. При n = 1 эквивалентное этому равенство было найдено еще в 19 в. Существует обобщение теоремы Серра на случай когомологий произвольных когерентных пучков на полных алгебраич. многообразных (см. [1], [4]). В частности, когда многообразие X есть подмногообразие Коэна-Маколея (напр., локально полное пересечение) коразмерности d в неособом проективном многообразии Y, имеет место Д. между k-пространством Hⁱ(X, ℱ) и пространством глобальных Ext'oв

Ext^n-i(X; ℱ, ω̃_X)

где ℱ - когерентный пучок на X, 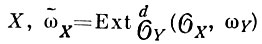(дуализирующий пучок Гротендикa), a n = dim X. При этом пучок ω̃_X является обратимым в том и только в том случае, когда X есть схема Горенштейна (см. Горенштейна кольцо).

Этальные когомологии. Пусть X - полное связное неособое алгебраич. многообразие размерности d над алгебраически замкнутым полем k, n - целое число, взаимно простое с характеристикой поля k, ℱ - локально свободный (в этальной топологии) пучок ℤ/nℤ-модулей на X, μ_n - пучок корней n-й степени из единицы. Существует невырожденное спаривание ℤ/nℤ-модулей [6]:

Нⁱ(X, ℱ) × H^2d-i(X, Ноm(ℱ, μ^⊗d_n)) → ℤ/nℤ.

Более общая теорема Д. относится к гладким, но необязательно полным многообразиям [5]. Существует невырожденное спаривание ℤ/nℤ-модулей

Hⁱ_c(X, ℱ) × H^2d-i(X, Ноm(ℱ, μ^⊗d_n)) → ℤ/nℤ,

где слева стоят когомологий с компактными носителями. Если поле k есть алгебраич. замыкание поля k', X = X' ⊗_k' k и ℱ = ℱ' ⊗_k' k, то группа Галуа Gal(k/k') действует на Hⁱ(X, ℱ) и предыдущее спаривание есть спаривание Gal(k/k')-модулей.

Аналогом первой из приведенных теорем Д. для l-адических когомологий является теорема двойственности Пуанкаре: существует невырожденное спаривание ℤ_l-модулей

Hⁱ(X, ℤ_l) × H^2d-i(X, ℤ_l[d]) → ℤ_l,

где ℤ_l[d] - пучок Тейта, неканонически изоморфный пучку ℤ_l (см. l-адические когомологий). Отсюда следует изоморфизм ℚ_l-пространств

Hⁱ(X, ℚ_l) ≅ Ноm(H^2d-i(X, ℚ_l)(d), ℤ_l)

и, в частности, равенство чисел Бетти

b_i(Х; l) = b_2d-i(Х; l).

Так же, как и в случае когомологий когерентных пучков, имеется обобщение предыдущих результатов на относительный случай собственного морфизма схем, формулируемый на языке производных категорий [6].

Другие теории когомологий. Аналоги теоремы Пуанкаре имеют место для теории кристальных когомологий [7], когомологий де Рама над полем нулевой характеристики [8]. В теоретико-числовых приложениях важную роль играют когомологии пучков на плоской топологии Гротендика числовых схем. В отдельных частных случаях для таких когомологий также имеются теоремы Д. [9].

Лит.: [1] Гротендик А., в сб.: Международный математический конгресс в Эдинбурге, М., 1962, с. 116-37; [2] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 10, М., 1972, с. 47-112; [3] Серр Ж.-П., в сб. переводов: Расслоенные пространства и их приложения, М., 1958, 372-450; [4] Наrtshоrnе R., Residues and duality, В., 1966; [5] Théorie des topos et cohomologie étale des schémas, t. 3, В., 1973; [6] Verdier J. L., в кн.: Proceedings of a Conference on Local Fields, В., 1967, S. 184-98; [7] Berthelot P., Cohomologie cristalline des schémas de caractéristique p > 0, В., 1974; [8] Hartshorne R., Ample subvarieties of algebraic varieties, В., 1970; [9l Mazur В., «Amer. J. Math.», 1970, v. 92, p. 343-61; [10] Altman А., Кleiman S., Introduction to Grothendieck duality theory, В., 1970.

И. В. Долгачев.

2) Д. в алгебраической топологии - положение, когда значения одних топологич. инвариантов определяют значения других. Д. в алгебраич. топологии выражается: в Д. (в смысле теории характеров) между группами гомологии и когомологии одной и той же размерности при двойственных группах коэффициентов; в изоморфизме между группами гомологии и когомологий дополнительных размерностей многообразия (Пуанкаре двойственность); в изоморфизме между группами гомологии и когомологий взаимно дополнительных множеств пространства (Александера двойственность); во взаимозаменяемости в определенных ситуациях гомотопических и когомотопических, а также гомологич. и когомологич. групп, к-рая без дополнительных ограничений на размерность пространства имеет место не для обычных, а для S-гомотопич. и S-когомотопич. групп (см. S-двойственностъ).

Д. между гомологиями и когомологиями состоит в следующем. Пусть {Н_r(Х, А), f_*, ∂} - произвольная гомологии теория над нек-рой допустимой категорией пар пространств и их отображений, т. е. система, удовлетворяющая Стинрода-Эйленберга аксиомам теории гомологии с дискретной или компактной абелевой группой H_r(Х, А). Тогда система {H^r(Х, А), f^*, ∂}, где H^r(X, А) - группа характеров группы H_r(Х, А), а f^* и δ - гомоморфизмы, сопряженные соответственно гомоморфизмам f_* и ∂, удовлетворяет аксиомам Стинрода-Эйленберга теории гомологии и стало быть представляет собой теорию когомологии над той же категорией с компактной или, соответственно, дискретной группой Н^r(Х, А). Подобным же образом для каждой теории когомологии может быть построена двойственная теория гомологии. Следовательно, теории гомологии и когомологии составляют двойственные пары; при этом, преобразование одной теории в другую, с точностью до естественных эквивалентностей, является инволюцией. Для любой теоремы теории гомологии, т. е. теоремы относительно системы {H_r(X, А), f, ∂}, существует двойственное утверждение относительно системы {H^r(X, А), f^*, ∂}, т. е. теорема теории когомологии, и наоборот. При переходе к двойственному утверждению группы заменяются их группами характеров, гомоморфизмы меняют направление, подгруппы заменяются факторгруппами, и наоборот. Примерами могут служить сами аксиомы Стинрода-Эйленберга. В случае конкретных категорий или теорий построение этой Д. осуществляется, напр., следующим образом. Пусть K = {t^r} (конечный) комплекс. За произведение r-мерной цепи с_r комплекса К над дискретной или компактной группой X коэффициентов и r-мерной коцепи e^r комплекса K над группой X^* коэффициентов, двойственной X в смысле теории характеров, принимается число mod 1

(c_r, c^r) = ∑_t^r∈K c_r(t^r) c_r(t^r).

Это произведение определяет умножение класса гомологии с классом когомологии и превращает r-мерные группы гомологии и когомологии в группы характеров одна другой. На бесконечных комплексах имеются группы двух видов - проекционные и спектровые. Спектровые группы гомологии являются пределами прямых спектров групп гомологии замкнутых подкомплексов, упорядоченных по возрастанию, а проекционные группы гомологии - гомологич. группами пределов прямых спектров из групп цепей указанных подкомплексов. Группы когомологий получаются аналогично, как пределы соответствующих обратных спектров. При дискретной группе коэффициентов обе гомологич. группы совпадают и дают группу гомологии конечных циклов, а при компактной группе совпадают когомологич. группы и дают группу когомологий бесконечных коциклов. Д. в случае конечных комплексов порождает Д. проекционных групп между собой и спектровых групп между собой, а эти последние Д. (посредством сингулярных комплексов, нервов покрытий и т. п.) - Д. r-мерной проекционной (соответственно спектровой) группы гомологии H_r(R, X) пространства R над дискретной или компактной группой X коэффициентов в какой-либо теории (сингулярных гомологии, Александрова - Чеха гомологий и когомологий, Вьеториса гомологий и т. п.) с r-мерной проекционной (соответственно спектровой) группой когомологий H^r(R, X^*) в той же теории над группой X^* двойственной X (см. К [3], [6], [9]):

H_r(R, X)|H^r(R, X^*) при Х|Х^*.

Соотношения между инвариантами, выражающими связности дополнительных размерностей многообразия, были установлены в первой же работе по алге-браич. топологии - в статье А. Пуанкаре (Н. Poincaré, 1895), где было показано, что для n-мерного ориентируемого многообразия его р-мерное и (n - р)-мерное числа Бетти равны друг другу, равно как и р-мерный и (n - р - 1)-мерный коэффициенты кручения. Эта теорема была усилена О. Вебленом (О. Veblen, 1923), сформулировавшим ее для баз гомологии, а применение групп когомологий придало ей форму, полнее выражающую содержание этой Д. Для получения этой формы следует поставить в соответствие каждой r-мерной цепи с_r, заданной на какой-либо триангуляции К гомологического n-мерного ориентированного многообразия Мⁿ и принимающей значения из дискретной или компактной группы X коэффициентов (n - р)-мерную коцепь с^n-p клеточного комплекса K^* из барицентрических звезд K, принимающую на какой-либо звезде то значение, которое с_p имеет на соответствующем этой звезде симплексе. Сказанное соответствие, в силу совпадения групп комплексов K и K^*, определяет изоморфизм групп гомологии и когомологий [дополнительных размерностей многообразия Мⁿ:

Нг(Мⁿ, Х) ~ Н^n-r(Мⁿ, X).

При этом X может быть и модулем, а в случае неориентируемого многообразия теорема верна по модулю 2. Замена группы H^n-r(Мⁿ, X) двойственной ей группой H_n-r(Мⁿ, X^*) приводит к Д. [1]:

H_r(Mⁿ, X) | H_n-r(Mⁿ, X^*), при Х | Х^*,

представляющей интерес еще и тем, что при ней произведением оказывается индекс пересечения циклов, произвольно выбранных из перемножаемых классов (см. [1], [11], [12], [13], [15], [16]).

Большой этап, вначале теоретико-множественный, по отысканию топологич. свойств множества, к-рые определялись бы топологич. свойствами его дополнения, завершился теоремой, полученной Дж. Александером (J. Alexander, 1922) и утверждающей, что r-мерное число Бетти mod 2 полиэдра, лежащего в n-мерной сфере, равно (n - r - 1)-мерному числу Бетти mod 2 дополнения (см. Александера двойственность). В свою очередь, эта теорема положила начало ряду исследований, в сильной мере повлиявших на развитие всей алгебраич. топологии. Исследования велись в направлении обобщения классов пространств (плоскость, евклидовы пространства, сферы и многообразия любых размерностей, локально компактные пространства и т. д.), их подмножеств (полиэдры, замкнутые подмножества, произвольные подмножества) и областей коэффициентов (целые числа по модулю 2, группа целых чисел, поле рациональных чисел, другие конкретные группы и поля, произвольная абелева группа, топологич., в основном компактные, абелевы группы и т. п.), для к-рых имеет место двойственность Александера, а также усиления тех соотношений, к-рые связывают инварианты взаимно дополнительных множеств (равенство чисел Бетти, изоморфизм групп, Д. топологических групп, естественные и связывающие гомоморфизмы и т. п.). Ряд полученных результатов может быть представлен в виде диаграммы (см. [1], [3], [4], [5], [6], [7], [8], [9], [11]):

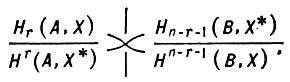
где X - дискретная или компактная группа коэффициентов, Х^* | Х, А и В -взаимно дополнительные множества n-мерного сферич. многообразия Мⁿ, H_r(A, X) и H^r(A, X^*) - r-мерные группы гомологии и когомологий (с компактными носителями) Александрова - Чеха множества А над X и соответственно X^*, а Н_n-r-1(В, Х^*) и H^n-r-1(В, X) суть (n-r-1)-мерные спектровые группы гомологии и когомологии Александрова - Чеха множества В над X^* и соответственно над X. Указанные в диаграмме соотношения, полученные различными авторами и различными способами, согласованы в том смысле, что соответствующие при изоморфизмах элементы представляют собой один и тот же характер остальных групп при вертикальных и горизонтальных Д. Таким образом, они являются различными формами одной и той же теоремы двойственности. Верхняя двойственность есть Д. зацепления, т. е. при ней произведением элементов является зацепления коэффициент циклов, произвольно выбранных из перемнежаемых классов или, в случае компактной группы X^*, определяется по непрерывности зацеплением циклов. В приведенной диаграмме группы первого столбца могут быть заменены (r+1)-мерными группами гомологии и когомологий Стинрода с компактными носителями, а группы второго столбца - (n-r-1)-мерными проекционными группами гомологии и когомологии Александрова - Чеха; тогда, в случае компактного А изоморфизм главной диагонали дает теорему двойственности Стинрода в ее первоначальном виде, если когомологич. группу множества В заменить, по теореме Пуанкаре, (r+1)-мерной группой гомологии бесконечных циклов. Если группа X компактна, то диаграммы изоморфны; если, кроме того, и множество А компактно, то двойственность верхней строки диаграммы представляет собой теорему, полученную Л. С. Понтрягиным в 1934 ([1], см. Понтрягина двойственность). О дальнейших обобщениях и направлениях см. [10], [14], [15], [16].

Важным видом двойственности Александера, касающимся связывающего гомоморфизма и аксиомы точности, является изоморфизм между группами гомологии, а также между группами когомологии соседних размерностей. Эти изоморфизмы, установленные П. С. Александровым и А. Н. Колмогоровым, утверждают, что r-мерная группа гомологии (соответственно когомологий) замкнутого множества А нормального локально бикомпактного пространства R, ацикличного в размерностях r и r+1, над компактной (соответственно дискретной) группой X изоморфна (r+1)-мерной группе гомологии (соответственно когомологии) дополнения:

H_r(A, X) ~ H_r+1(R\A, X) и

H^r(A, X) ~ H^r+1(R\A, X).

Из этих изоморфизмов выводится теорема Понтрягина. П. С. Александров [2] получил эти изоморфизмы из общих соотношений Д., связывающих группы гомологии и когомологии взаимно дополнительных множеств и пространства, а также ядра, образы и факторгруппы этих групп при их естественных гомоморфизмах вложения н высечения. Эти соотношения несут также много другой важной информации о расположении множеств в пространстве. П. С. Александров [2] получил их с помощью спектровых групп гомологии и когомологий относительно так называемых особых подкомплексов нервов, состоящих из симплексов, замыкания вершин которых некомпактны. А. Н. Колмогоров доказал вышеуказанные изоморфизмы Д. посредством так называемых функциональных групп гомологий и когомологий (см. Колмогорова двойственность). Указанные выше и другие Д. (напр., Лефшеца двойственность) связаны между собой различными соотношениями. Они могут быть рассмотрены и как следствия нек-рой общей Д., в к-рой участвуют так называемые внешние группы множества, являющиеся прямым пределом групп когомологии окрестностей этого множества, упорядоченных по вложению (см. [3], [4], [5], [6], [7], [12], [13]). Связи между различными Д. приобретают новый вид при их рассмотрении с помощью пучков теории.

Лит.: [1] Понтрягин Л. С., «Успехи матем. наук», 1947, т. 2, в. 2, с. 21-44; [2] Александров П. С., «Изв. АН СССР. Сер. матем.», 1942, т. 6, с. 227-82; [3] его же, «Матем. сб.», 1947, т. 21, № 2, с. 161-232; [4] его же, «Тр. Матем. ин-та АН СССР», 1955, т. 48, с. 1-108; 1959, т. 54, с. 1-136; [5] Чогошвили Г. С., «Докл. АН СССР», 1946, т. 51, № 2, с. 87-90; [6] его же, «Успехи матем. наук», 1966, т. 21, в. 4, с. 23-34; [7] Kарlan S., «Trans. Amer. Math. Soc.», 1947, v. 62, p. 248-71; [8] Ситников К. А., «Матем. сб.», 1954, т. 34, с. 3-54; 1955, т. 37, с. 385-434; 1959, т. 48, с. 213-26; [9] Берикашвили Н. А., «Тр. Тбил. матем. ин-та», 1957, т. 24, с. 409-84; [10] Баладзе Д. С., там же, 1972, т. 41, с. 41-83; [11] Bourgin D., Modern Algebraic Topology, N. Y.-L., 1963; [12] Спеньер Э., Алгебраическая топология, пер. с англ., М., 1971; [13] Switzer R. M., Algebraic Topology Homotopy and Homology, В.-Heid.-N. Y., 1975; [14] Скляренко Е. Г., «Изв. АН СССР. Сер. матем.», 1971, т. 35, № 4, с. 831-43; [15] Воrеl A., Moore J. С., «Michig. Math. J.», 1960, v. 7, p. 137-60; [16] Bredon G. E., Sheaf Theory, N. Y., [1967].

Г. С. Чогогивили.

3) Д. в теории аналитических пространств - двойственность между различными векторными топологич. пространствами когомологий комплексных пространств. Имеются три типа теорем Д., соответствующие двойственностям Пуанкаре, Лефшеца и Александера-Понтрягина в топологии, но относящиеся к пространствам когомологий Н^p_Ф(Х, ℱ) комплексного пространства X со значениями в когерентном аналитич. пучке ℱ и носителями в семействе Ф или их факторпространствам (см. Когомологий со значениями в пучке).

Первому типу принадлежит теорема двойственности Серра [1]. Пусть X - комплексное многообразие размерности n со счетной базой, Ω - пучок голоморфных дифференциальных форм степени n, a ℱ - локально свободный аналитич. пучок на X. Для каждого целого р, 0 ≤ р ≤ n, определено билинейное отображение

Н^p(X, ℱ) × Н^n-p_c(X, Hom(ℱ, Ω)) → ℂ, (*)

которое можно записать как композицию ∪-умножения

Н^p(X, ℱ) × Н^n-p_c(X, Ноm(ℱ, Ω)) → Нⁿ_c(X, Ω)

(с означает семейство компактных носителей) и линейной формы s на Hⁿ_c(Х, Ω), называемой следом и имеющей вид

s(ω̂) = (-1)ⁿ∫_Xω,

где ω - форма типа (n, n) с компактным носителем, отвечающая классу ω̂ в силу теоремы Дольбо (см. Дифференциальная форма). Теорема двойственности Серра утверждает, что если наделить пространства когомологий канонической локально выпуклой топологией (см. Когерентный аналитический пучок), отображение (*) непрерывно по первому аргументу при условии отделимости пространства Н_p+1(Х, ℱ) устанавливает изоморфизм векторных пространств:

(H^p(Х, ℱ))' ≅ Н^n-p_c(X, Ноm(ℱ, Ω)).

Пучки ℱ и Ноm(ℱ, Ω) можно поменять ролями, поскольку операция Ноm(⋅, Ω) на локально свободных пучках инволютивна.

В частности, если многообразие X компактно, канонический, a D - любой дивизор на X, то из теоремы Серра вытекает равенство размерностей пространств H^p(X, 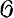_X(D)) и Н^n-p(Х, 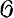_X(K-D)), к-рое часто используется при вычислениях с когомологиями. Известна аналогичная теорема Д. для неособых проективных алгебраич. многообразий над произвольным полем (см. Двойственность в алгебраич. геометрии)

В случае, когда ℱ - произвольный когерентный аналитич. пучок на многообразии X, имеет место естественная топологич. Д. между отделимыми пространствами, ассоциированными с векторными топологич. пространствами H^p_Ф(X, ℱ) и Ext^n-p_Ψ(X; ℱ, γ), где Ф -семейство замкнутых носителей, Ψ - семейство компактных носителей или наоборот, а через Ext^n-p_Ψ(X; ℱ, γ) обозначены производные функтора Hom_Ψ(X; ℱ, ⋅). При этом пространство H^p_Ф(X, ℱ) отделимо одновременно с Ext^n-p+1_Ψ(X; ℱ, γ) (см. [2], [3]). Для компактного X отсюда следует изоморфизм конечномерных пространств

(Н^p(X, ℱ))' ≅ Ext^n-p(X; ℱ, Ω). Если X - многообразие Штейна, то получается топологич. Д. между H⁰(X, ℱ) и Extⁿ_c(X; ℱ, Ω) и между

H^p_c(X, ℱ) и Ext^n-p(X; ℱ, Ω).

Имеется также обобщение этих результатов на случай комплексных пространств с особенностями [4] и на относительный случай [5], аналогичное соответствующим теоремам Д. в алгебраич. геометрии.

Аналогом теоремы Лефшеца является следующая теорема Д. [3]: пусть X - комплексное многообразие со счетной базой размерности n, K - штейнов компакт в X. Для любого когерентного аналитич. пучка ℱ на X и любого целого р ≥ 0 пространство Ext^n-p(K; ℱ, Ω) имеет топологию типа DFS (сильно сопряженное к пространству Фреше-Шварца), а его сопряженное пространство алгебраически изоморфно H^p_K(X, ℱ). Другая теорема того же типа [6]: в тех же предположениях, если Y ⊂ X открыто, то пространство H^p_Y(X, ℱ) имеет топологию типа QFS (факторпространства Фреше - Шварца), Ext^n-p_c(Y; ℱ, Ω) имеет топологию типа QDFS (факторпространства типа DFS), а ассоциированные с ними отделимые пространства находятся в топологич. Д. Пространство H^p_Y(X, ℱ) отделимо одновременно с Ext^n-p+1_c(Y; ℱ, Ω).

Третий тип теорем Д. представлен следующей теоремой [8]: для любого открытого подмножества Y ⊂ X = ℂР¹ - сильное сопряженное к пространству Г(Y, 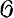_X/Г(Х, 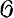_X)) изоморфно Г(Х\Y, 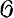_X). Эта теорема допускает следующее обобщение [7]: пусть X - n-мерное комплексное многообразие, счетное на бесконечности, Y ⊂ X открыто, ℱ - когерентный аналитич. пучок на X, р ≥ 0 - целое число. Рассматриваются канонич. отображения векторных топологич. пространств

α : H^p(Х, ℱ) → H^p(Y, ℱ), γ : Н^p+1_X\Y(Х, ℱ) → Н^p+1(Х, ℱ), β : Ext^n-p+1_c(X; ℱ, Ω) → Ехt^n-p-1_c(X\Y; ℱ, Ω).

Для того чтобы отделимое пространство, ассоциированное с Соkеr β, было изоморфно сильному сопряженному к Соkеr α, необходимо и достаточно, чтобы Кеr γ было замкнуто. (Известен пример, когда Кеr γ не замкнуто.) В частности, если пучок ℱ локально свободен и

Н^p(Х, ℱ) = Н^p+1(Х, ℱ) = 0, то отделимые пространства, ассоциированные с Н^p(Y, ℱ) и Н^n-p-1(X\Y, Hom (ℱ, Ω)), находятся в Д.

Лит.: [l] Serre J.-P., «Comm. math. helv.», 1955, t. 29, M. 9-26; [2] Malgrange В., Séminaire Bourbaki, 1962/63, p. 246; [3] Banica C., Stanasila O., Metode algebrice in teoria globala a spatiilor complexe, Bucuresti, 1974; [4] Ramis J. P., Ruget G., «Publ. IHES», 1970, t. 38, p. 77-91; [5] их же, «Invent. math.», 1974, Bd 26, № 2, S. 89-131; [6] Головин В. Д., "Функциональный анализ", 1971, т. 5, № 4, с. 66; [7] его же, «Матем. заметки», 1973, т. 13, № 4, к. 561; [8] Grothendieck A., «J. reine und angew. Math.», 1953, Bd 122, № 1, S. 35.

В. П. Паламодов.

4) Д. в теории аналитических функций.

а) Преобразование Бореля. Э. Борелю (Е. Borel, 1895) принадлежит идея преобразования каждого ряда вида:

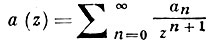
в ряд

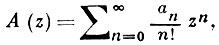
и обратно, при условии

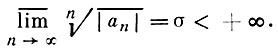
Так устанавливается отношение Д. между функциями, аналитическими в окрестности бесконечно удаленной точки |z| > σ и целыми функциями экспоненциального типа σ. На этом пути, напр., получается теорема Пойа: пусть k(φ) - опорная функция выпуклой оболочки множества особенностей функции a(z) (при аналитическом продолжении на полуплоскость вида Re(ze^-iφ) > с, а

h(φ) = lim̅_r→∞ (ln |A(re_iφ)| / r)

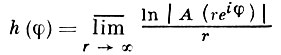
- индикатор роста целой функции A (z); тогда

h(φ) = k(-φ), σ ≤ φ ≤ 2π.

В силу этого отношения двойственности задача аналитич. продолжения функции a(z) в круг |z| < σ эквивалентна изучению роста соответствующей целой функции A(z) по различным направлениям.

б) Д. в пространствах аналитич. функций. Пусть G - открытое множество расширенной комплексной плоскости ℂ и A(G) - пространство всех аналитических в G функций с топологией, задаваемой системой норм

р_n(f)= max_z∈Kn |f(z)|, f ∈ A(G),

где {K_n} - возрастающая система компактных множеств, содержащихся в G и исчерпывающих G; таким образом, сходимость f_n→f в A(G) означает равномерную сходимость f_n(z) → f(z) на всех компактных подмножествах G. Пусть ∞ ∈ G, A₀(G) - подпространство A(G), для функций к-рого f(∞) = 0, и F - компактное подмножество ℂ̅. Рассматривается система ^F всех открытых множеств G ⊃ F и множество функций ∪_G∈^F A(G).

Две функции f₁(z) и f₂(z) из этого множества считаются эквивалентными, если совпадают их сужения на нек-рое множество G ∈ ^F. Введенное отношение эквивалент-

ности разбивает всю рассматриваемую совокупность на классы f̅. Каждый класс наз. локально аналитической на F функцией, и совокупность таких функций обозначается A(F). Класс A(F) естественным образом превращается в линейное пространство, и в нем вводится топология индуктивного предела последовательности нормированных пространств В_n. Последние строятся следующим образом. Пусть {G_n} - убывающая последовательность множеств из ^F такая, что G_n+1 ⊂ G_n и ∀G ∈ ^F

∃n₀: n ≤ n₀ ⇒ G_n ⊂ G.

Тогда B_n - пространство ограниченных в G_n аналитич. функций с нормой

||f|| = max_z∈Gn |f(z)|.

Простейший факт о Д. пространств аналитических функций состоит в следующем. Пусть G - открытое множество и (для определенности) ∞ ∈ G, a F = ℂ̅\G. Двойственным (сопряженным) к пространству A₀(G) (в смысле теории линейных топологич. пространств) является пространство A(F). Эта Д. устанавливается следующим образом: если Λ(f) - непрерывный линейный функционал над A₀(G), то существует единственный элемент g̅ ∈ A(F) такой, что

Λ(f) = ∫_γ f(z)g(z) dz,

где γ - некоторый (сложный) контур, идущий в G и охватывающий F, a g ∈ g̅ (Λ(f) нe зависит от g(z) ∈ g̅). Пространства А (Е) могут быть определены для произвольных множеств E ⊆ ℂ, а не только для рассмотренных здесь случаев, когда E = G - открытое множество и E = F - компакт. Дальнейшие обобщения: рассмотрение множеств на римановых поверхностях, пространств функций многих комплексных переменных, пространств векторнозначных аналитич. функций (со значениями в линейных топологич. пространствах).

Развитие теории Д. пространств аналитич. функций, с одной стороны, стимулировалось развитием общей теории Д. линейных топологич. пространств, а с другой стороны, само стимулировало развитие общей теории выявлением глубоких конкретных закономерностей. Применения Д. пространств аналитич. функций многообразны: вопросы интерполяции и аппроксимации (см. ниже), аналитическое продолжение, разделение и устранение множеств особенностей, интегральные представления различных классов функций.

в) Д. между теоремами полноты и единственности. Полнота системы элементов {f_n} какого-либо локально выпуклого пространства X имеет место в том и только том случае, когда для произвольного линейного непрерывного в X функционала Λ из Λ(f_n) = 0, n = 1, 2, ..., следует Λ ≡ 0. Этот факт

приводит к установлению связи между проблемами полноты в пространствах аналитич. функций и разного рода теоремами единственности для аналитич. функций. С функционалом Λ связывается (ср. п. 1) нек-рая аналитич. функция F(z). Условие Λ(f_n) = 0, n = 1, 2, ..., приводит к равенству нулю F(z) в нек-рых точках или к равенству нулю коэффициентов F(z). Теоремы единственности позволяют заключить, что F(z) = 0, а затем и что функционал Λ = 0. Для пространств аналитич. функций в круге был сформулирован следующий принцип двойственности проблем единственности и полноты. Пусть А_R и А_P - соответственно пространства функций, аналитических в кругах: |z| < R и |ζ| < Р, где 0 < R, Р ≤ ∞ и F(z, ζ) - функция, аналитическая в бицилиндре: |z| < R, |ζ| < P. Пусть L и Λ_ζ - линейные функционалы, определенные в А_R и А_P, и пусть ⊂ A_R и Ω ⊂ A_P - подмножества функций, представимых соответственно в виде Λ_ζ F(z, ζ) и L_zF(z, ζ). Последовательность функции Λ_{ζ n}F(z, ζ)

будет полной в 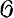тогда и только тогда, когда для каждой φ(ζ) ∈ Ω из Λ_{ζ n}φ =0, n = 0, 1, 2, ..., следует: φ(ζ) ≡ 0.

В частности, когда R = P = ∞ и F(z, ζ) = е^zζ, оба множества 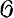и Ω совпадают с совокупностью всех целых функций экспоненциального типа.

г) Д. в экстремальных задачах теории функций. Известно, что задачи наилучшего приближения в нормированных пространствах двойственно связаны с нек-рыми линейными экстремальными задачами. Так, если Е - подпространство в нормированном пространстве X и ω - произвольный элемент X, то

sup_{l∈E^⊥,||l||≤1} l|(ω)| = inf_x∈E ||ω - х||, (1)

где E^⊥ - аннулятор Е, т. е. совокупность линейных функционалов l, обращающихся в нуль на элементах Е. Соотношение (1), устанавливаемое на основании теоремы Хана-Банаха, оказалось впоследствии частным случаем двойственных связей экстремальных задач математич. программирования. Пусть G есть n-связная область, граница ∂G к-рой состоит из спрямляемых контуров, В¹ - класс аналитических в G функций f(z), |f(z)| ≤ 1, Е¹ - класс аналитических в G функций, представимых интегралом Коши через свои граничные значения, ω(ζ) - какая-либо интегрируемая функция на ∂G. Имеет место равенство:

sup_f∈B¹ |∀_∂G f(ζ) ω(ζ) dζ| = inf_φ∈E¹ ∀_∂G |ω(ζ) - φ(ζ)| |dζ| (2)

Слева в этом соотношении стоит линейная экстремальная задача для ограниченных функций (напр., при ω(ζ) = 1/(2πi(ζ - z₀)²) получают задачу о sup_f∈B¹|f'(z₀)| - задачу о «лемме Шварца» - в многосвязной области); справа - задача наилучшего приближения произвольной функции ω(ζ) на ∂G граничными значениями аналитич. функций в интегральной метрике. Соотношение (2) служит отправным пунктом для проникновения в каждую из двух экстремальных задач, содержащихся в нем: с его помощью устанавливаются характеристич. свойства экстремальных функций f^*(z) ∈ B¹ и φ^*(z) ∈ E¹, исследуется вопрос об их единственности и т. д. Функция f^*(z) оказывается наделенной важными геометрич. свойствами: в задаче о лемме Шварца она отображает G на n-листный круг; в других задачах с ω(ζ), аналитической на ∂G, функция f^*(z) отображает G на m≥n-листный круг (см. [2]-[4]).

Лит.: [1] Маркушевич А. И., Избранные главы теории аналитических функций, М., 1976; [2] Итоги науки. Математический анализ. 1964, М., 1966, с. 76-164; [3] Итоги науки. Математический анализ. 1967, М., 1969, с. 75-132; [4] Итоги науки. Математический анализ. 1963, М., 1965, с. 5-80; [5] Исследования по современным проблемам теории функций комплексного переменного, М., 1960, с. 77-95.

А. И. Маркушевич, С. Я. Хавинсон.

5) Д. в теории топологических векторных пространств - тройка {F, G, f}, в к-рой F, G - векторные пространства над полем K, f - билинейный функционал (форма) в F×G, обладающий свойством отделимости: если f(x, y) = 0 для каждого у, y ∈ G, то х = 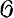; если f(x, у) = 0 для каждого х, x ∈ F, то y = 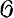. Говорят также, что форма f осуществляет Д., а пространства F, G находятся в Д., или образуют дуальную пару; если f фиксирована, то пишут f(x, у)= (х, у). Важнейшим примером является естественная двойственность: F = (F, τ) - локально выпуклое топологическое векторное пространство с топологией τ, G = (F, τ)' - сопряженное пространство всех линейных τ-непрерывных функционалов в F и (х, х') = х'(х) при x ∈ F, х' ∈ G; свойство отделимости для этой формы (. , .) вытекает, напр., из локальной выпуклости топологии τ (теорема о достаточном числе функционалов - следствие теоремы Хана - Банаха). Теория Д. изучает в основном способы построения объектов в F или G, дуальных (двойственных) заданным относительно формы (. , .); соответствия между свойствами взаимно дуальных объектов; топологии, порождаемые Д. Основным инструментом этого изучения является аппарат поляр (при K = ℝ или ℂ полярой множества А, A ⊂ F наз. множество

A^o = {y ∈ G: Re(x, у) ≤ 1, ∀ х ∈ А}).

Д. порождает различные локально выпуклые топологии на F (и равным образом на G); такие, напр., как слабая топология σ(F, G) (порожденная заданной Д.), задаваемая семейством полунорм |(⋅, у)|, y ∈ G, это - слабейшая топология, при к-рой все отображения (⋅, у) непрерывны; топология Макки μ(F, G) с базой окрестностей нуля, образованной полярами А^o абсолютно выпуклых σ(G, F)-компактных подмножеств А в G; сильная топология τ^*(F, G), база к-рой образована полярами А⁰ ограниченных подмножеств А в (G, σ(G, F)). Для любого А, A ⊂ F множество А⁰⁰ является выпуклой σ(F, G)-замкнутой оболочкой множества A ∪ {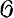} (теорема о биполяре). Пространство G совпадает с (F, τ(F, G))' (основная теорема теории Д., показывающая, что любую Д. можно интерпретировать как естественную). Пространство (F', σ(F', F)) наз. слабым сопряженным с F.

Пусть F - локально выпуклое пространство над ℝ или ℂ. Для ограниченности множества A, A ⊂ F, необходимо и достаточно каждое из условий: а) А ограниченно в слабой топологии; б) А⁰ - поглощающее множество. Если А - окрестность, то A⁰ является σ(F', F)-компактом. Метризуемое пространство F полно в том и только в том случае, когда замкнутость множества A, A ⊂ F', в топологии σ(F', F) равносильна замкнутости в той же топологии всех пересечений A ∩ U⁰, где U - окрестность нуля в F (теорема Крейна-Шмульяна). Если F - полное сепарабельное пространство и f - линейный функционал в F', то f ∈ (F', σ(F', F))' тогда и только тогда, когда из условия lim_n x_n = 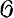в топологии σ(F', F) следует lim_n(x_n) = 0 (теорема Гротендика). Подмножество А полного пространства F относительно σ(F, F')-компактно, если оно относительно σ(F, F')-секвенциально компактно (теорема Эберлейна). Выпуклое подмножество А пространства Фреше над ℝ σ(F, F')-компактно тогда и только тогда, когда для любого f, f ∈ F', существует а, а ∈ А такое, что sup_A f = f(a) (теорема Джеймса). Для того чтобы (F, σ)' = G, необходимо и достаточно условие: топология τ не слабее топологии σ(F, G) и не сильнее топологии μ(F, G) (теорема Макки - Аренса, дающая важное в приложениях описание топологий, сохраняющих Д.). Каждое из следующих условий на пространство (F, τ) достаточно для совпадения τ с топологией Макки: а) F - бочечное пространство, б) - борнологическое пространство (в частности, метризуемое). Сильная топология τ^* (F, G), вообще говоря, не сохраняет Д.; если X = G локально выпукло и X' = F, то пространство X^* = (X', τ^*(X', X)) наз. сильным сопряженным с X, и в случае, когда τ^*(Х', X) сохраняет Д. (т. е. Х^*' = Х), пространство X наз. полурефлексивным (X - рефлексивное пространство, если Х^** = Х).

Если Н -подпространство F, то {Н, G/H⁰} и {F/H, Н⁰} - дуальные пары относительно естественных факторизации формы (⋅, ⋅). Если задано семейство Д. {F_α, G_α, (⋅, ⋅)_α}, то Д. произведения пространств F = ∏_αF_α и подпространства G = ∏^*_αG^*_α всех финитных семейств из ∏_αG_α осуществляет форма

(f, g) = ∑_α (f_α, g_α)_α,

где

f = {f_α} ∈ ∏_αF_α, g = {g_α} ∈ ∏^*_α G_α.

Подобным же образом описывается Д. индуктивного и проективного пределов lim_α ind F_α, lim_α pr F_α. Наличие в пространствах F, F_α топологий, сохраняющих Д., позволяет истолковать эти утверждения как описание естественных Д. для ∏_αF_α (тихоновская топология), F/H (фактортопология), Н (индуцированная топология), lim_α ind F_α и lim pr F_α, соответственно. В случае нормированного пространства F естественный изоморфизм Н^* и F^*/H⁰ является изометрией:

||f | H|| = dist(f, H⁰), f ∈ F^*.

Использование Д. в конкретных задачах линейного анализа пропорционально той роли, какую играют в этих задачах линейные (непрерывные) функционалы. Особенно заметными (если не определяющими) являются идеи теории Д. в следующих разделах анализа: в исследовании линейно топологических (метрических) свойств локально выпуклых пространств и, в частности, описании естественной Д. для данного пространства [1] - [3], [5], в теории обобщенных функций [4], в теории экстремальных задач [6] - [7], в спектральной и структурной теории линейных операторов [1], [2] в теоремах полноты и единственности в теории аналитических функций, в теории аналитических функционалов Фантапье [8], см. также Двойственность в теории аналитических функций.

Лит.: [1] Бурбаки Н., Топологические векторные пространства, пер. с франц., М., 1959; [2] Робертсон А. П., Робертсон В.-Дж., Топологические векторные пространства, пер. с англ., М., 1967; [3] Шефер X., Топологические векторные пространства, пер. с англ., М., 1971; [4] Данфорц Н., Шварц Дж., Линейные операторы, пер. с англ., т. 1, М., 1962, т. 2, М., 1966; [5] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961; [6] Иоффе А. Д., Тихомиров В. М., Теория экстремальных задач, М., 1974; [7] Рокафеллар Р., Выпуклый анализ, пер. с англ., М., 1973; [8] Хавин В. П., Итоги науки. Математический анализ. 1964, М., 1966, с. 76-164; [9] Хавинсон С. Я., «Успехи матем. наук», 1963, т. 18, в. 2, с. 25-98; [10] Diestеl J., Geometry of Ваnасh spaces-selected topics, В.-N.Y., 1975.

H. И. Никольский.

6) Д. в экстремальных задачах и выпуклом анализе - особенность выпуклых множеств, выпуклых функций и выпуклых экстремальных задач, состоящая в возможности задавать их двояким образом - в основном и сопряженном пространствах. Замкнутые выпуклые множества в локально выпуклом топологич. векторном пространстве допускают двойственное описание: они совпадают с пересечением замкнутых полупространств, их содержащих. Это позволяет связать с каждым выпуклым множеством А в векторном пространстве X двойственный объект в сопряженном пространстве - его поляру А⁰ = {х^* ∈ Х^* : 〈х*, х〉 ≤ 1, х ∈ А}. Замкнутые выпуклые функции (т. е. функции с выпуклыми и замкнутыми надграфиками) в локально выпуклом топологич. векторном пространстве также допускают двойственное описание: они являются поточечными верхними гранями аффинных функций, их не превосходящих. Такая Д. позволяет связать с каждой выпуклой функцией f : X → ℝ̅ двойственный объект - сопряженную функцию, заданную на сопряженном пространстве X^* и определяемую формулой

f^*(x^*) = sup (〈x^*, x〉 - f(x)).

Поточечные верхние грани линейных функций в локально выпуклом топологич. векторном пространстве суть выпуклые замкнутые однородные функции, и в этом факте заложена Д. между выпуклыми множествами и выпуклыми однородными функциями. В основании описанных Д. лежат теоремы Хана - Банаха о продолжении линейных функционалов и теоремы отделимости выпуклых множеств.

Сущность двойственного задания выпуклых множеств и выпуклых функций находит свое отражение в инволютивности оператора полярности А⁰⁰ = А и сопряжения f^** = f, имеющей место для выпуклых замкнутых множеств, содержащих нуль, и выпуклых замкнутых функций, всюду больших - ∞. Последний результат, касающийся функций (наз. теоремой Фенхеля-Моро), порождает многочисленные теоремы Д. для экстремальных задач линейного и выпуклого программирования. Примером пары двойственных задач являются следующие две задачи линейного программирования

I. (с, х) → inf; II. (b, y) → sup (1)

Ax ≥ b, x ≥ 0; A^*y ≤ c, y ≥ 0.

Здесь

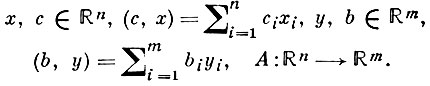
Для пары двойственных задач линейного программирования имеет место следующая альтернатива: либо значения задач конечны и равны и в обеих задачах существует решение, либо в одной из задач множество допустимых значений пусто или значение задачи бесконечно.

Обычный прием построения двойственной задачи состоит в следующем. Задача минимизации

f(х) → inf, х ∈ X, (2)

где X - линейное пространство, f : X → ℝ̅, включается в класс подобных ей задач, зависящих от параметра:

F(х, у) → inf, х ∈ X, где Y - некоторое другое линейное пространство, F: X × Y → ℝ̅, F(x, 0) = f(x) (функцию F наз. возмущением f). Обычно F предполагается выпуклой. Двойственной к задаче по отношению к данному возмущению наз. задача

-F^*(0, у^*) → sup, у^* ∈ Y^*, (2*)

где F^* - функция, двойственная (сопряженная) с F в смысле Лежандра - Юнга - Фенхеля. Для простейших задач выпуклого программирования типа

f₀(x) → inf, f_i(x) ≤ 0, i = 1, ..., m, x ∈ В, (3)

где X - линейное пространство, f_i : X → ℝ̅ - выпуклые функции на X, В - выпуклое множество в X (частными случаями (3) являются задачи линейного программирования), обычно применяются следующие стандартные возмущения, зависящие от параметров y ∈ ℝ̅^m, y = (y₁, ..., y_m), f₀(x) → inf, f_i(x) ≤ y_i, i = 1, ..., m, x ∈ B. Теоремы двойственности для общих классов задач выпуклого программирования утверждают, что при нек-рых допущениях на возмущение F значения задач (2) и (2*) совпадают, и более того, решение одной из задач является множителем Лагранжа для другой.

Лит.: [1] Minkowski Н., Geometrie der Zahlen, Lpz.- В., 1910; [2] eго же, Gesammelte Abhandlungen, Bd 1-2, Lpz.-В., 1911; [3] Fenchel W., «Canad. J. Math.», 1949, v. 1, p. 73-77; [4] Рокафеллар P., Выпуклый анализ, пер. с англ., М., 1973; [5] Ekeland I., Teman R., Convex Analysis and Variational Problem, N. Y., 1976; [6] Иоффе А. Д., Тихомиров В. M., Теория экстремальных задач, М., 1974.

В. М. Тихомиров.

7) Д. конечных абелевых групп - классический прототип общей Понтрягина двойственности и различных более поздних ее модификаций. Относится к свойствам изоморфного соответствия между конечной абелевой группой А и группой А̂ = Ноm(А, k^*) ее характеров со значениями в мультипликативной группе k^* алгебраически замкнутого поля k характеристики, не делящей порядок группы А (см. Характеров

группа). Естественное отображение f: А → А̂, определенное правилом

f(a)(χ) = χ(a)

для всех а ∈ А, χ ∈ А̂, также является изоморфизмом, причем для любой подгруппы В ⊆ А имеет место равенство f(B) = (В^⊥)^⊥, где

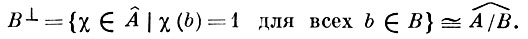
Соответствие В → В^⊥ устанавливает двойственность между решетками подгрупп групп А и А̂. Это соответствие взаимно однозначно и обладает свойствами

(BC)^⊥ = B^⊥ ∩ C^⊥, (B ∩ C)^⊥ = B^⊥C^⊥.

Лит.: [1] Понтрягин Л. С, Непрерывные группы, 3 изд., М., 1973, гл. 6; [2] Huppert В., Endliche Gruppen I., В., 1967, S. 688-96.

А. И. Кострикин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.