
ДВОЙНОГО СЛОЯ ПОТЕНЦИАЛ
ДВОЙНОГО СЛОЯ ПОТЕНЦИАЛ - выражение вида u(x) = ∫Г ∂/∂ny (h(rxy))μ(y)dsy, (1)
где Г - граница произвольной ограниченной N-мерной области g ⊂ EN, N ≥ 2, ny - внешняя по отношению к области g нормаль к границе Г в точке у, μ(у) - плотность потенциала - функция, заданная на Г, h(rxy) - фундаментальное решение уравнения Лапласа
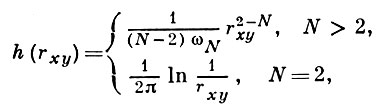
ωN = 2(√π)N/Г(N/2) - площадь поверхности единич-ной (N-1)-мерной сферы, 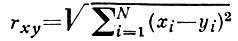 - расстояние между точками х и y ∈ EN. Граница Г принадлежит классу С(1,λ) она является поверхностью или дугой Ляпунова.
- расстояние между точками х и y ∈ EN. Граница Г принадлежит классу С(1,λ) она является поверхностью или дугой Ляпунова.
Выражение (1) может быть истолковано как потенциал, создаваемый диполями, помещенными на Г, направление к-рых в каждой точке у ∈ Г совпадает с направлением внешней нормали ny, а интенсивность равна μ(у).
Если μ(y) ∈ С(0)(Г), то u(х) определено для всех х ∈ EN (в частности и для х ∈ Г) и обладает следующими свойствами.
1) Всюду в EN\Г функция u(х) имеет производные всех порядков ( ∈ C(∞)) и удовлетворяет уравнению Лапласа, причем производные по координатам точки х можно вычислять дифференцированием под знаком интеграла.
2) При переходе через границу Г функция u(х) испытывает разрыв. Пусть х0 - произвольная точка на Г, u+(х0) и u- (х0) - предельные значения изнутри и извне, тогда u±(х0) существуют и равны
U±(x0) = ± μ(x0)/2 + ∫Г ∂/∂ny (h(rx0y)) μ(y) dsy, (3)
причем интеграл в формуле (3) как функция х0 ∈ Г принадлежит С(0,α) при любом 0 ≤ α < 1, кроме того, функция, равная u в g и u+ на Г, непрерывна в g + Г, а функция, равная u в EN - (g + Г) и u- на Г, непрерывна в EN - g.
3) Если плотность μ(y) ∈ С(0,α) и α ≤ λ, то u(х), продолженная так же, как в 2) на g + Г или EN - g, принадлежит классу С(0,α) в g + Г или в EN - g.
4) Если α > 1 - λ, а х1 и х2 - две точки, принадлежащие нормали, выходящей из точки х0, симметричные относительно точки х0, то
limx1→x0 (∂u(x2)/∂n - ∂u(x1)/∂n) = 0. (4)
В частности, если существует одна из производных ∂u(х0)/∂n, ∂-(х0)/∂n, то существует и другая и ∂u+(х0)/∂n = ∂u-(х0)/∂n. Это свойство справедливо также, если μ(y) ∈ С(0)(Г), а Г ∈ С(2).
Перечисленные выше свойства обобщаются во многих направлениях. Плотность μ(х) может принадлежать Lp(Г), р ≥ 1. Тогда u(x) ∈ Lp(g + Г), u(х) ∈ С(∞) вне Г и удовлетворяет уравнению Лапласа, формулы (3) и (4) имеют место для почти всех х0 ∈ Г и интеграл в (3) принадлежит Lp(T).
Изучены также свойства Д. с. п., понимаемых как интегралы по произвольной мере ν, определенной на Г:
u(x) = ∫Г ∂/∂ny (h(rxy)) dν(y);
здесь также u(x) ∈ C(∞) вне Г и удовлетворяет уравнению Лапласа, формулы (3) и (4) имеют место для почти всех х0 ∈ Г по мере Лебега ν(x) с заменой μ(х0) на производную меры ν' (х0). В определении (1) фундаментальное решение уравнения Лапласа может быть заменено на произвольную функцию Леви для общего эллиптич. оператора 2-го порядка с переменными коэффициентами, а ∂/∂ny - на производную по конормали. При этом остаются справедливыми свойства, перечисленные выше (см. [2]).
Д. с. п. играет важную роль в решении краевых задач для эллиптич. уравнений. Представление искомого решения (первой) краевой задачи в виде Д. с. п. с неизвестной плотностью μ(у) и использование свойства 2) приводит к интегральному Фредголъма уравнению второго рода на Г для определения функции μ(у) (см. [1], [2]).
При решении краевых задач для параболич. уравнений используется понятие теплового потенциала двойного слоя, т. е. интеграл вида
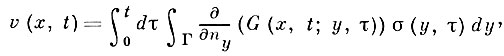
где G(x, t; у, τ) - фундаментальное решение уравнения теплопроводности в N-мерном пространстве:
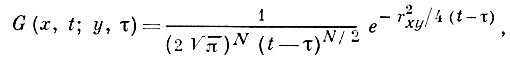
σ(у, τ) - плотность потенциала. Функция v(x, t) и ее обобщение на случай произвольного параболич. уравнения 2-го порядка обладают свойствами, аналогичными указанным выше для u(х) (см. [3], [4], [5]).
Лит.: [1] Гюнтер Н. М., Теория потенциала и ее применение к основным задачам математической физики, М., 1953; [2] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [3] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966; [4] Смирнов В. И., Курс высшей математики, 5 изд., т. 4, М., 1958; [5] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968.
И. А. Шигимарев.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'