ДВОЙНАЯ ТОЧКА

ДВОЙНАЯ ТОЧКА - один из видов особых точек кривой F(x, у) = 0, в к-рой первые частные производные равны нулю и по крайней мере одна из вторых частных производных функции F(x, у) не равна нулю. При исследовании строения кривой вблизи Д. т. рассматривают знак выражения

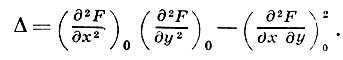
Если Δ > 0, то Д. т. наз. изолированной точкой; напр., у кривой

у² - х⁴ + 4х² = 0

начало координат есть изолированная Д. т. (см. рис. 1). Если Δ < 0, то Д. т. наз. узловой, или точкой самопересечения; напр., у кривой

(х² + у² + а²)² - 4а²х² - а⁴ = 0

начало координат есть узловая точка (см. рис. 2). Если Δ = 0, то Д. т. кривой является либо изолированной, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную: например, а) точка

возврата 1-го рода - ветви кривой расположены по разные стороны от общей касательной и по одну сторону от общей нормали (см., напр., рис. 3; у² - х³ = 0); б) точка возврата 2-го рода - ветви кривой расположены по одну сторону от общей касательной и по одну сторону от общей нормали (см., напр., рис. 4; (у - х²)² - х⁵ = 0); в) точка самоприкосновения - ветви кривой соприкасаются (см.,

напр., рис. 5; у² - x⁴ = 0).

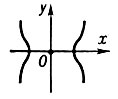
Рис. 1.

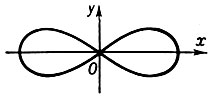
Рис. 2.

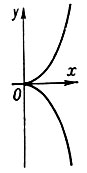
Рис. 3.

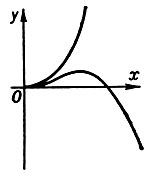
Рис. 4.

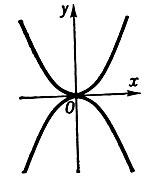
Рис. 5.

А. Б. Иванов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.