ДВИЖЕНИЕ

ДВИЖЕНИЕ - преобразование пространства, сохраняющее геометрич. свойства фигур (размеры, форму и др.). Понятие Д. сформировалось путем абстракции реальных перемещений твердых тел в евклидовом пространстве. Д. принимается иногда в качестве основного понятия при аксиоматическом построении геометрии.

Д. евклидова пространства - преобразование пространства, сохраняющее расстояние между точками. Д. наз. собственным (Д. первого рода) или несобственным (Д. второго рода) в зависимости от того, сохраняет оно или не сохраняет ориентацию пространства.

На плоскости собственные Д. выражаются аналитически в прямоугольной системе координат (х, у) при помощи следующих формул

х̃ = х cos φ - у sin φ + а,

у̃ = х sin φ + y cos φ + b,

показывающих, что совокупность всех собственных Д. на плоскости зависит от трех параметров а, b, φ. Первые два параметра характеризуют параллельный перенос плоскости на вектор (а, b), а параметр φ - вращение (поворот) плоскости вокруг начала координат. Собственное Д. представляет собой произведение (композицию) вращения вокруг начала на угол φ и параллельного переноса на вектор (а, b). Всякое собственное Д. может быть представлено либо как параллельный перенос, либо как вращение вокруг некоторой точки.

Несобственные Д. выражаются при помощи формул

х̃ = х cos φ + у sin φ + а,

у̃ = х sin φ - y cos φ + b,

показывающих, что несобственное Д. есть произведение собственного Д. на преобразование симметрии относительно нек-рой прямой. Всякое несобственное Д. представляет собой произведение параллельного переноса вдоль нек-рого направления и симметрии относительно прямой, имеющей то же направление.

В пространстве собственное Д. есть или вращение вокруг оси, или параллельный перенос, или может быть представлено в виде произведения вращения вокруг оси и параллельного переноса в направлении этой оси (винтовое Д.). Несобственное Д. есть либо симметрия относительно плоскости, либо может быть представлено в виде произведения симметрии относительно плоскости на вращение вокруг оси, перпендикулярной к этой плоскости, либо - в виде произведения симметрии относительно плоскости на перенос в направлении вектора, параллельного этой плоскости.

В прямоугольной системе координат (x, у, z) в пространстве Д. выражается аналитически при помощи формул

х̃ = а₁₁x + а₁₂у + a₁₃z + а, у̃ = а₂₁х + а₂₂y - a₂₃z + b,

z̃ = а₃₁х + а₃₂y - a₃₃z + c,

где элементы матрицы |a_ij| удовлетворяют следующим

условиям ортогональности

a_1ra_1s + a_2ra_2s + a_3ra_3s = δ_rs

(δ_rs = 1 при r = s, δ_rs = 0 при r ≠ s). Д. является собственным или несобственным в зависимости от того, равняется ли определитель этой матрицы 1 или -1. См. Ортогональное преобразование.

Аналогично в случае n-мерных евклидовых пространств Д. выражается аналитически в прямоугольных координатах при помощи ортогональной матрицы A = ||a_ij||:

a_1ra_1s + a_2ra_2s + ... + a_nra_ns = δ_rs.

Д. рнманова пространства - взаимно однозначное непрерывно дифференцируемое отображение класса C^s, s ≥ 2, при к-ром сохраняются длины соответствующих линий. Линейный элемент пространства

ds² = g_αβ (х₁, х₂, ..., х_n) dx^αdx^β,

где по индексам α, β производится суммирование, инвариантен относительно Д. Аналитически Д. определяется формулами, выражающими координаты преобразованной точки М̃(х̃ⁱ) через координаты исходной точки М(хⁱ) при помощи функций fⁱ(x) класса C^s:

x̃^α = f^α(x¹, х², xⁿ), (*)

а = α = 1, 2, ..., n. (*)

Условие инвариантности линейного элемента означает, что

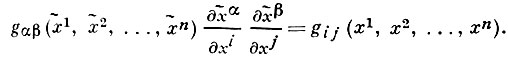
Важное значение имеет понятие Д. в римановых пространствах общей теории относительности: в сильных асимметрических гравитационных полях твердые тела могут иметь лишь весьма ограниченные движения. Возможны также случаи, когда они не будут вовсе допускать никаких Д. В последней ситуации при любом преобразовании пространства метрика не остается инвариантной. Другими словами, любое перемещение сопровождается деформацией тела.

Д. пространства аффинной связности - взаимно однозначное непрерывно дифференцируемое отображение класса C^s, s ≥ 2, при к-ром всякое поле параллельных векторов вдоль любой гладкой линии переходит в поле параллельных векторов преобразованной кривой. При Д. объект аффинной связности Г^α_βγ(x) переходит в себя. Обратно, всякое отображение (*), переводящее объект аффинной связности в себя, есть Д.

Д. составляют группу преобразований (см. Движений группа). Они являются простейшими преобразованиями пространства.

Лит.: [1] Егоров И. П., Лекции по аксиоматике Вейля и неевклидовым геометриям, Рязань, 1973; [2] его же, Движения в пространствах аффинной связности, Казань, 1965; [3] Базылев В. Т., Дуничев К. И., Иваницкая В. П., Геометрия, т. 1, М., 1974.

И. П. Егоров.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.