ДАРБУ ТЕНЗОР

ДАРБУ ТЕНЗОР - симметрический тензор третьей валентности

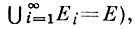
где b_αβ - коэффициенты второй квадратичной формы поверхности, K - гауссова кривизна, а b_αβγ и K_α - их ковариантные производные. К этому тензору в специальных координатах впервые пришел Г. Дарбу [1]. С Д. т. связана кубическая дифференциальная форма:

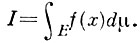
Эта форма, отнесенная к кривой на поверхности, наз. инвариантом Дарбу. На поверхности постоянной отрицательной кривизны инвариант Дарбу совпадает с дифференциальным параметром на любой ее кривой. Кривая, в каждой точке к-рой инвариант Дарбу равен нулю, наз. линией Дарбу. На нелинейчатой поверхности отрицательной кривизны существует одно действительное семейство линий Дарбу. На поверхности положительной кривизны существуют три действительных семейства линий Дарбу. Поверхность, в каждой точке к-рой Д. т. определен и тождественно равен нулю, наз. поверхностью Дарбу. Поверхности Дарбу являются поверхностями 2-го порядка, не развертывающимися на плоскость.

Лит.: [1] Darboux G., «Bull. sci. math.», 1880, ser. 2, t. 4, p. 348-84; [2] Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 2, М.-Л., 1948, стр. 210-33.

Е. В. Шикин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.