ДАРБУ СУММА

ДАРБУ СУММА - сумма специального вида. Пусть действительная функция f(x) определена и ограничена на отрезке [а, b], τ = {x_i}^i=k_i=0 - его разбиение:

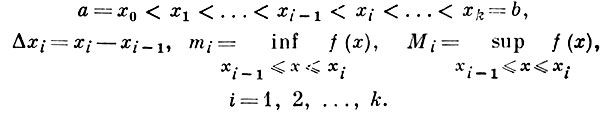
Суммы

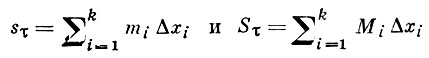
наз. соответственно нижней и верхней интегральной Д. с. Для любых двух разбиений τ и τ' отрезка [а, b] справедливо неравенство s_τ ≤ S_τ', т. е. любая нижняя Д. с. меньше верхней. Если

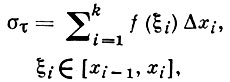
- интегральная сумма Римана, то

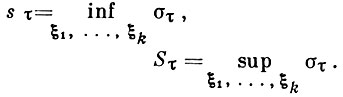
Геометрич. смысл нижней и верхней Д. с. заключается в том, что они равны площадям ступенчатых фигур, состоящих из прямоугольников с основаниями длины Δx_i и высотами соответственно m_i и М_i (см. рис.). Эти фигуры в случае, когда f(х) ≥ 0, аппроксимируют изнутри и извне криволинейную трапецию, образованную графиком функции f(x), осью абсцисс и отрезками прямых х = а и х = b (которые могут вырождаться в точки).

Величины

I_* = sup_τ s_τ и I^* = inf_τ S_τ (1)

наз. соответственно нижним и верхним интегралом Дарбу. Они являются пределами нижних и верхних Д. с:

I_* = lim_δτ→0 s_τ, I^* = lim_δτ→0 S_τ,

где

δ_τ = max_i=1,2,...,k Δx_i

- мелкость разбиения τ. Условие

I_* = I^* (2)

является необходимым и достаточным для того, чтобы функция f(x) была интегрируема по Риману на отрезке [а, b]. При этом в случае выполнения условия (2) значение нижнего и верхнего интегралов Дарбу совпадает с интегралом Римана

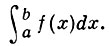
Условие (2) с помощью Д. с. может быть сформулировано в следующей эквивалентной форме: для любого ε > 0 существует такое разбиение τ, что S_τ - s_τ < ε.

Условие

lim_δτ→0 (S_τ - s_τ) = 0

также является необходимым и достаточным для интегрируемости по Риману функции на отрезке [а, b]. При этом

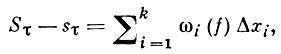
где ω_i(f) - колебание функции f(x) на отрезке [x_i-1, x_i], i = 1, 2, ..., k.

Понятие нижних и верхних Д. с. обобщается на случай функций многих переменных, измеримых в смысле нек-рой положительной меры μ. Пусть Е - измеримое (напр., по Жордану или по Лебегу) множество n-мерного пространства n = 1, 2, ..., 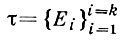- разбиение множества Е, т. е. система таких измеримых множеств Е, что

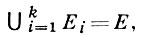
(3)

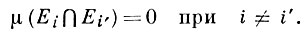
(4)

Пусть функция f ограничена на множестве Е,

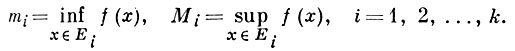
(5)

Суммы

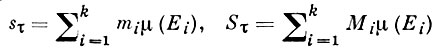
(6)

также наз. нижней и, соответственно, верхней Д. с. Нижний I_* и верхний I^* интегралы определяются по формулам (1). В случае меры Жордана их равенство является необходимым и достаточным условием интегрируемости функции по Риману, причем их общее значение совпадает с интегралом Римана. В случае же меры Лебега для ограниченных измеримых по Лебегу функций всегда

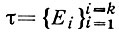Вообще, если μ - полная σ-аддитивная мера, определенная на σ-алгебре , f - ограниченная μ-измеримая на Е действительная функция, - разбиение множества на μ-измеримые множества Е_i, удовлетворяющие условиям (3), (4), Д. с. s_τ и S_τ определяются по формулам (5) - (6), а интегралы I_* и I^* - по формулам (1), в к-рых везде под μ понимают рассматриваемую меру, то

I_* = I^* = ∫_E(x) dμ.

Обобщением Д. с. для неограниченных μ-измеримых функций f, определенных на множествах , являются ряды (если они абсолютно сходятся)

(7)

где 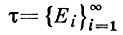- разбиение множества Е ∈ 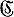_μ (это разбиение состоит, вообще говоря, из бесконечного числа μ-измеримых множеств удовлетворяющих

условию (4) и, конечно, таких, что а m_i и М_i определяются по формулам (5), при этом в формулах (7) (как и выше в формулах (6)) считается, что ∞ ⋅ 0 = 0 ⋅ ∞ = 0. Если снова определить I_* и I^* по (1), понимая теперь s_τ и S_τ в смысле (7), то I_* = I^*, причем в случае, когда величина I = I_* = I^* является конечной,

функция f интегрируема по мере μ и I = ∫_E f(x)dμ. Названы по имени Г. Дарбу [1].

Лит.: [1] Darboux G., «Аnn. sci. Ecole Norm. supér.», 1875, ser. 2, t. 4, p. 57-112; [2] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1-2, М., 1971-73; [3] Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1-2, М., 1973; [4] Никольский С. М., Курс математического анализа, 2 изд., т. 1-2, М., 1975.

Л. Д. Кудрявцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.