ДАРБУ ИНВАРИАНТЫ СЕТИ

ДАРБУ ИНВАРИАНТЫ СЕТИ - выражения h и k.

h = c + ab - ∂a/∂u, k = c + ab - ∂b/∂v, составленные из коэффициентов уравнения Лапласа

(*)

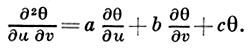
Уравнению (*) удовлетворяет каждая из однородных координат точки х, описывающей сопряженную сеть из линий u и v на двумерной поверхности проективного n-мерного пространства (n ≥ 3). Г. Дарбу [1] показал, что Д. и. с. h и k не меняют своего значения при изменении нормирования координат точки х. Накладывая то или иное условие на Д. и. с., получают частные виды сопряженных сетей.

Лит.: [1] Darboux G., Lecons sur la théorie générate des surfaces..., pt 2, P., 1889, [2] Tzitzeica G., Geometrie différentielle projective des réseaux, P.-Bucarest, 1924; [3] Фиников С. П., Теория конгруэнции, М.-Л., 1950.

В. Т. Базылев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.