ДАНЖУА ТЕОРЕМА

ДАНЖУА ТЕОРЕМА о производных числах: производные числа каждой конечной функции F(x) почти в каждой точке х удовлетворяют одному из следующих соотношений:

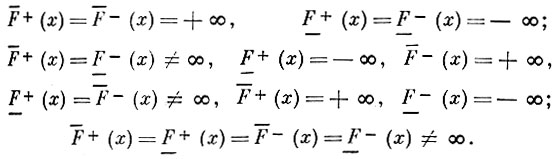
Доказана для непрерывных функций А. Данжуа [1]. Обобщением утверждения Данжуа является теорема [2]: для почти каждого х контингенция графика F(x) в точке (х, F(x)) является одной из следующих фигур: плоскость, полуплоскость (с невертикальной граничной прямой), прямая (невертикальная).

Лит.: [1] Denjoy A., «J. math. pures et appl.», 1915, Ser. 7, t. 1, p. 105-240; [2] Сакс С., Теория интеграла, пер. с англ., М., 1949.

Т. П. Лукашенко.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.